Mach's Conservation of Area and the Pythagorean Theorem

Ernst Mach (February 18, 1838 - February 19, 1916) was an Austrian physicist and philosopher who is popularly recognized for his research into wave propagation. Mach's number of a moving object is the ratio of the object's speed to that of sound. One of his early achievements was to construct an apparatus to verify Doppler's effect for sound waves.

Vladimir Lenin severely criticized Mach's view that science should be based solely on directly observable phenomena, branding it "hidden solipsism".

Albert Einstein considered Mach as the precursor of the general theory of relativity because of Mach's objections to Newton's concept of absolute space. Einstein even coined the term "Mach's Principle" to describe the idea that local phenomena can be explained in the framework of global structure of the universe.

Mach wrote [Space and Geometry, p. 71] that

... the mental experiment is never anything more than a copy of the physical experiment. The mental experiment would be impossible if physical experience had not antecedently led us to a knowledge of spacially unalterable physical bodies, - to the concept of measure.

By experiences of this character, we are conducted to the truth that of the six metrical magnitudes discoverable in a triangle (three sides and three angles) three, including at least one side, suffice to determine the triangle.

In this spirit, Mach proceeded with another example - the Pythagorean theorem. The essential point (a lemma in the math vernacular) is this:

If a triangle, a, b, c be slid along a short distance in its own plane,

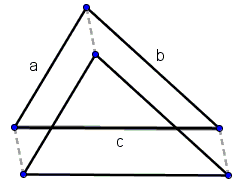
Mach's principle of conservation of the area

it is assumed that the space which it leaves behind is compensated for by the new space on which it enters. This is to say, that the area swept out by two of the sides during the displacement is equal to the area swept out by the third side. The basis for this conception is the assumption of the conservation of the area of the triangle.

Mach must have seen farther than I was immediately able to, so that I needed to fill in details in his argument. I have denoted the six areas in Mach's diagram with capital letters A through F:

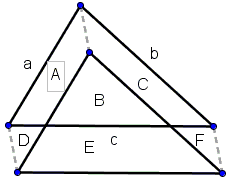
Mach's principle of conservation of the area in some detail

...it is assumed that the space which it leaves behind is compensated for by the new space on which it enters

A + C = E.
This is to say, that the area swept out by two of the sides during the displacement is equal to the area swept out by the third side

(A + D) + (C + F) = D + E + F.
The basis for this conception is the assumption of the conservation of the area of the triangle

A + B + C = B + E.

It is now clear that the three assertions are indeed equivalent. Mach now proceeds in the following fashion:

If an oblique-angled triangle having the sides a, b, and c be displaced in the direction of the side b, only a and c will, by the principle above stated, describe equivalent parallelograms, which are alike in an equal pair of parallel sides on the same parallels. If a makes with b a right angle, and the triangle is displaced at right angles to c, the distance c, the side c will describe the square c², while the two other sides will describe parallelograms the combined areas of which are equal to the area of the square.

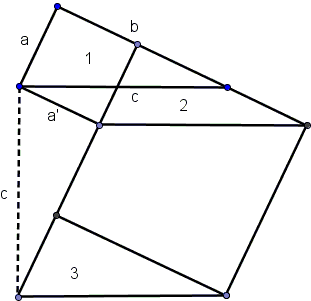
Mach's proof of the Pythagorean theorem

But the two parallelograms are, by the observation which just precedes, equivalent respectively to a² and b², - and with this the Pythagorean theorem is reached.

The theorem is reached, but I should confess that the derivation left me bewildered and dissatisfied. I did not feel being "conducted to the truth" in a manner intuitively obvious to me. It might have been to Mach (and probably it was) but his overreliance on his own sensations suggests to me that Lenin might have had a good point dubbing Mach a solipsist. On the other hand, I have a suspicion that A. Einstein would not accept Mach's proof wholeheartedly either. It lacks symmetry and simplicity, Einstein so valued.

I personally find extra argumentation beyond the reference to Euclid I.35 (Parallelograms which are on the same base and in the same parallels equal one another) superfluous. With the nod to Euclid I.35 there is just a shorter and, in my view, more intuitive derivation, see, for example, proofs #24 and #69 in the collection of other proofs.

(Stuart Anderson has considered a similar derivation based on area sweeps.)

Reference

E. Mach, Space and Geometry: In the Light of Physiological, Psychological and Physical Inquiry, Dover, 2004

71544603