Jan Stevens' proof of E. W. Dijkstra's Generalization of the Pythagorean Theorem

Jan Stevens' proof of E. W. Dijkstra's Generalization

If, in a ΔABC, angles α, β, γ lie opposite the sides of length a, b, c, then

(*)	sign(α + β - γ) = sign(a² + b² - c²),

In the proof of his generalization, Dijkstra ran into difficulties with geometric illustrations. As he himself wrote: Note that I carefully avoided the pictures for α + β > γ there are 9 of them ... As J. Stevens observes, The problem with this is that (*) involves negative areas and angles. What one can do in Euclidean geometry, is to compare positive quantities in size. ... To avoid negative quantities one can construct, instead of the difference the sum.


	α + β > γ	a² + b² > c².

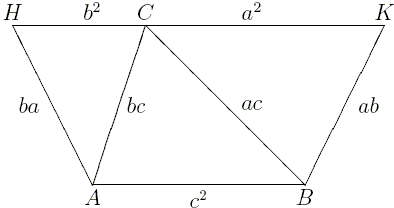
The diagrams make the construction obvious. ABKH is an isosceles trapezoid that degenerates in rectangle for the right angled triangle (see proof #41.) Dijkstra's formula follows from the following

Lemma

In an isosceles trapezoid, of the two bases, the base incident to smaller (base) angles is longer, and vice versa.

Proof

According to the Fifth Postulate, two lines traversed by a third meet on that side of the transversal for which the sum of the internal angles is less than two right angles (180°). This means that the point of intersection of the side lines AH and BK (say P) is closer to AB if α + β > γ and is closer to HK if α + β < γ. Noting that the triangle ABP and HKP are similar and that in one case AP = BP < HP = HK while in the other AP = BP > HP = HK, the corresponding inequalities hold also for the bases, AB and HK. To sum up,

a² + b² > c² iff α + β > γ,

or, which is the same if we exclude the equality case as in proof #41,

a² + b² < c² iff α + β < γ,

Dijkstra's identity is the combination of these three cases. In fact, there is no need to invoke proof #41. Indeed, since a² + b² < c² is equivalent to α + β < γ and a² + b² > c² to α + β > γ, the equality a² + b² = c² is necessarily equivalent to α + β = γ.

There is more than one way of handling the isosceles trapezoid ABKH. For example, draw the diagonal BH and consider two triangles ABH and KHB. The triangles have a pair of equal sides: AH = BK, with BH being common to both triangles. According to Euclid I.24, of the third sides that is bigger which subtends a bigger angle. (Euclid I.25 proves the converse.) However, in the two triangles,

∠ABH = ∠BHK,

so that AB > HK iff ∠HBK > ∠BHA iff ∠BKH < ∠BAH. This again proves the claim.

Jan Stevens actually proves more, viz.,

a² + b² - c² = 2ab sin( (α + β - γ)/2 ).

In case where α + β > γ the proof is based on the following diagram

where AE and BF are perpendicular to HK. Since α + β + γ = 180°, ∠FBK = 90° - γ = (α + β - γ)/2, making FK = ab sin (α + β - γ)/2. Since, obviously, EH = FK, the formula follows.

In case α + β < γ, the derivation is similar. The case of the right-angled triangle fits into the formula as well and can be referred to Proof 41.

The formula can be rewritten as

a² + b² - c² = 2ab cos γ,

giving an additional proof of the Cosine Law.

71940104