Euclid's Proposition I.7

Given two straight lines constructed from the ends of a straight line and meeting in a point, there cannot be constructed from the ends of the same straight line, and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each equal to that from the same end.

If possible, given two straight lines AC, CB constructed on the straight line AB and meeting at the point C, let two other straight lines AD, DB be constructed on the same straight line AB, on the same side of it, meeting in another point D and equal to the former two respectively, namely each equal to that from the same end, so that AC equals AD which has the same end A, and CB equals DB which has the same end B.

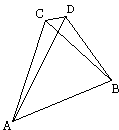
Join CD.

Since AC equals AD, therefore the angle ACD equals the angle ADC. Therefore the angle ADC is greater than the angle DCB. Therefore the angle CDB is much greater than the angle DCB.

Again, since CB equals DB, therefore the angle CDB also equals the angle DCB. But it was also proved much greater than it, which is impossible. (I.5).

Therefore given two straight lines constructed from the ends of a straight line and meeting in a point, there cannot be constructed from the ends of the same straight line, and on the same side of it, two other straight lines meeting in another point and equal to the former two respectively, namely each equal to that from the same end. Q.E.D

Note

This is pretty obvious that Euclid's argument very much depends ona specific type of configuration of the four points A, B, C, D as they appear arranged in the diagram above. The argument obviously fails for the diagram below:

It is absolutely possible to amend Euclid's argument by considering a few separate cases. But this is certainly cumbersome.

Euclid's Elements Reference Page

References

1. T. L. Heath, Euclid: The Thirteen Books of The Elements, Dover, 1956
2. R. Simson, The Elements of Euclid, Books I-VI, XI, XII + Euclid's Data, Elibron Classics, 2005