Kiselev's Geometry:
|

|
The book under review is an expanded translation of a unique phenomenon in the Russian mathematical literature. If nothing else, its staying power may serve an enticement to anyone interested in, or involved with, high school geometry. First published in 1892 by A. P. Kiselev as Elementary Geometry, by 1940 it underwent more than 40 revisions and eventually became a measuring rod for geometry education in Russia against which all other textbooks had to be judged. Its introduction to the English speaking student and teacher is more than welcome. The effort by Professor A. Givental who translated the book from Russian and combined pieces of the many editions of the original deserves a wholehearted recognition and sincere praise.
The early history of the book is murky. In the Tsarist Russia Kiselev's Geometry competed successfully against other textbooks. Its 23rd edition (1914) is available online. The upheaval of 1917 brought an overhaul of the education system based more on revolutionary zeal than on evolutionary societal demands. But towards the early 1930s the situation was ripe for a more rational attitude. On February 12, 1933, the Central Party Committee has issued a directive that instructed the responsible organizations to replace the "working (class) books" used in schools until then with specially designated "stable" textbooks (Math Education, n1 1934, p. 71). On November 16, 1936, the Mathematical Committee of the People's Commissariat of Education has branded the originally selected geometry book as an illiterate concoction of the lowest quality and recommended its immediate removal. The meeting of the Moscow Mathematical Society held on April 9, 1937 accepted a resolution expressing an outrage that the book has been yet republished for another year and recommended Kiselev's Geometry as a temporary replacement. For the 41st edition, Kiselev's Geometry has been edited by N. A. Glagolev.
The temporary replacement kept the official title until the mid 1950s. It appears that in 1955 the recognition has been awarded to the text authored by N. N. Nikitin and A. I. Fetisov. However, already in 1956 regrets have been sounded and the first time in 20 years it was noted that the Department of Education and the UchPedGiz (the official textbook publishing agency) all along were giving a wrong interpretation to the Central Committee's directive as if it really stipulated unique stable textbooks in every subject. Kiselev's Geometry has been allowed to stay around together with the new text until the latter underwent serious rework.
In time, Kiselev's Geometry stood its ground against textbooks by N. A. Izvolsky, V. G. Boltyansky and I. M. Yaglom, A. N. Kolmogorov, a translation of J. Hadamard's, a book written jointly by Nikitin and Fetisov, and then the books they wrote separately, and many others. The friends I polled who took geometry in the early 1960s all used Kiselev's book with an exception of experimental classes in special math schools that used the book by Fetisov. In later years, there was a serious competition from Nikitin's book but Kiselev's Geometry kept going on even if as a backup copy. I do not know whether by that time any book has been assigned an official status, but in a booklet Proofs in Geometry, first published in 1977, A. I. Fetisov while illustrating an erroneous proof notes dejectedly that the diagram is similar to the one used in an officially "approved book". There is no doubt as to what book he referred to.
From the discussions of 1955-1956 it appears that Kiselev's Geometry has been judged to follow too closely Euclid's Elements. As one example, it was pointed out that, by introducing the parallel postulate early on, the book by Nikitin and Fetisov managed to simplify the treatment of the Exterior Angle Theorem compared to its treatment in Kiselev's Geometry. There is no doubt that the wind of change in geometry education that began blowing in Europe at the end of the 19th century, has reached and influenced the Russian policy makers. In this particular instance of the Exterior Angle Theorem, it is usually cited as a great insight of Euclid's who postponed using the Fifth Postulate until I.29. He accordingly split the theorem into two parts, the first of which did not require parallel lines. The true appreciation of Euclid's sequence came with the 19th century development of various geometries, Absolute Geometry in particular. To a teacher a theorem of such significance provides a rich background for historical and philosophical discussion that most students are capable of appreciating.
In this context, Kiselev follows in Euclid's footsteps and delays introducing the Parallel Postulate until the second quarter of the book. (Unfortunately, while proving the absolute part of the theorem, he also repeats Euclid's argument, the argument that by Kisilev's time was found to be lacking in rigor imposed by the 19th century mathematics.) He does not follow Euclid blindly, though. Geometric objects are introduced each in its time, not at the beginning of the book. Their properties are defined when they become needed or are about to be proved. Kiselev also goes to some length to clarify general notions, like theorem and axiom, explains the relation between a theorem and its converse, inverse, and contrapositive statements, and proof by contradiction. Many sections are preceded by short introductions.
Sometimes the divergence from the Elements is significant as, for example, in his treatment of the Pythagorean theorem. He proves the theorem only after the theory of proportions. And the proof (p. 152) is a simplified version of Euclid's VI.31, to which the translator gives special attention towards the end of the book. Along with the full version of VI.31 we find there Euclid's I.47 and a proof by rearrangement. Kiselev's is the choicest selection among a great variety of the proofs of the famous theorem.
The book was originally written in a clear, no-nonsense style which has been polished over its many editions and revisions. The style was well preserved in the translation. There is nothing in the book that may even occasionally distract from the subject.
The most shining example is Kiselev's treatment of the circumference and π. Circumference is defined (p.202 as a limit of perimeters of the regular polygons inscribed into the circle when the number of sides is doubled indefinitely. Does not sound impressive? But consider then that Kiselev goes to a considerable length by preceding the definition with a reasonably developed theory of limits (pp. 195-199). The book gives a very clear introduction into the theory of limits which, although not 100% rigorous, neither noticeably cuts corners. For example, the book does prove that the limit (which is the circumference) exists (p. 202). This comes after a thorough discussion of similarity (pp. 117-182). In particular, he proves (p. 187) that regular polygons with the same number of sides are similar, and their sides have the same ratio as their radii or apothems. Combining this with the theory of limits he derives (p. 204) the fact that the ratio of the circumference to the diameter is the same for all circles and thus introduces π.
Simple as this may appear, even the best of the modern high school geometry texts make a mess of the definition of π. For example, H. Jacobs (Geometry, 3rd ed, p. 592) defines π as a limit of the ratio of the side to twice the radii of a regular polygon as the number of sides increases. And this after constructing a table for several polygons and observing the behavior of the ratio. Thus the definition of π and the determination of its value are combined into one, while the reason for the existence of π is not discussed at all.
Another topic that drew my attention is the irrationality of the square root of 2. Incidentally, the proof is remarkably similar to the one recently published by Tom Apostol (The American Mathematical Monthly, v 107, n 9, pp 841-842):
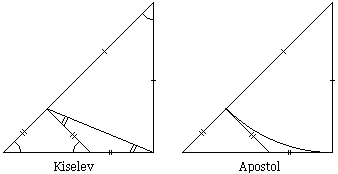 |
Unlike Apostol's, Kiselev's proof does not qualify as a proof without words and requires some leg work, but appeals to the same geometric ideas. However, this is not exactly the reason I like Kiselev's treatment. Kiselev precedes his proof with the notion of mensuration and a complete discussion of the Euclidean algorithm including Archimedes' Axiom. The proof is then followed by articles on lengths of segments, approximation, irrational numbers and the number line.
In the Translator's Foreword, Professor Givental mentions three virtues of a good textbook (precision, simplicity, conciseness) formulated yet by Kiselev himself, and adds a fourth one -- competence in the subject. Thinking specifically of Kiselev's Geometry, one other feature must be mentioned: autonomy of the discourse.
Every textbook is created for a particular audience which is usually characterized by the level of preparedness to absorb the material, both in terms of the requisite knowledge and the ability to do so. The requirements are usually set up in the introduction and commonly are violated in the text. This is done tacitly or with a reference to the imposed limitations on the size or the scope of the book. One salient virtue of Kiselev's Geometry is that, throughout, the author remains faithful to his intended audience, viz., middle and junior high school students taking up geometry for the first time. Assuming only very basic knowledge of mathematics, Kiselev builds a geometry edifice from the bottom up supplying both bricks and mortar in the process. The book is very much self-contained. The only outside references come at the upper storey, as for example, when he only mentions Gauss' constructibility theorem for regular polygons without proof.
The book comes with nearly 600 exercises distributed all over the book. Some are supplied with hints but none with a solution. I do not believe Kiselev had an intention or a pedagogical reason to conceal solutions from the student. In the Introduction to the first edition, he mentions a then available problem collection from which he drew exercises. In my time, another problem collection, with all the exercises solved, has been used alongside Kiselev's Geometry. While I do think that the absence of a solution key in the first English edition may deter some potential users, I do not believe it should. On one hand, in the body of the book, Kiselev devotes considerable time to solving problems, paying special attention to a variety of basic constructions. The text is interspersed with remarks on problem solving and methods of proof all of which come with practical demonstrations. On the other hand, at this time and day and access to the internet, an interested student can easily get a solution to a problem or two or an advice to help with a solution. There is a multitude of online forums that exist just to this end.
The book is light and relatively small, but due to Kiselev's concise, no-frills style, the topics covered are awarded comprehensive treatment. The book will serve well geometry students and teachers, homeschoolers, student teachers and their instructors. All should be looking forward to the appearance of the stereometry part of Kiselev's Geometry.
|Up| |Contact| |Front page| |Contents|
Copyright © 1996-2018 Alexander Bogomolny73509936
