Properties of the Figures in Euclid I.47
The basic diagram that accompanies Euclid I.47 held quite naturally a lasting interest over the centuries.
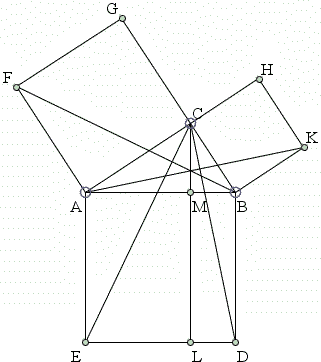
|
Some properties of the diagram and its generalizations have been already described, see Bride's Chair. Here I'll list a few more properties that came to my attention more recently.
Let U denote the intersection of AK and CD and V the intersection of CE and BF. Let C(ABDE) be the circle circumscribed around square ABDE. Then both U and V lie on that circle. (Solution is on a separate page.)
AC² + CD² = BC² + CE².
This follows from the previous property an the Law of Cosines. Let U be the intersection of AK and CD and V the intersection of CE and BF. AK⊥CD and CE⊥BF. From the Law of Cosines in triangles ACD and BCE, we have:
AD² = AC² + CD² - 2 CV·CD BE² = BC² + CE² - 2 CU·CE Since AD = BE, to prove the property, we only need to show that
CV·CD = CU·CE. But, by the previous property, points U and V lie on the circumcircle of the square ABDE.CV·CD = CU·CE then follows by the Intersecting Secants theorem.DK² = AC² + 4 BC².
Apply the Law of Cosines in ΔCDK and also in ΔACD:
DK² = CK² + CD² - 2 CV·CD AD² = AC² + CD² - 2 CV·CD. Subtracting the second from the first gives
DK² = CK² + AD² - AC² = 2BC² + 2AB² - AC² = 2BC² + 2(AC² + BC²) - AC² = AC² + 4 BC². DK² + EF² = 5 AB².
Assuming DK² = AC² + 4 BC², by symmetry, we then also have
EF² = BC² + 4 AC². In view of the Pythagorean theorem, adding the two gives the required result.Four times the sum of the squares of the medians from A and B equals 5AB².
We know that the lengths of ma, the median from A, and mb, the median from B, can be found from
ma² = (b² + c²)/2 - a²/4, mb² = (a² + c²)/2 - b²/4. Adding the two gives
ma² + mb² = c² + (a² + b²) / 4 = c² · 5 / 4. Let AK and BC cross in X, BF and AC cross in Y. Then
CX = CY and, in addition, if CXZY is a square, then Z lies on AB.The proof appears on a separate page.
DK² + GH² + EF² = 3 (AB² + BC² + AC²) [Exercices, p. 736].
This is a direct consequence of DK² + EF² = 5 AB² and
GH = AB. Area(EDKHGF) = 2(AC² + AC·BC + BC²).
All four triangles ABC, BDK, CGH, AFE have the same area AC·BC/2. The claim follows immediately from the Pythagorean theorem.
References
- F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991
- H. S. Hall, F. H. Stevens, A text-book of Euclid's elements for the use of schools, MacMillan & Co, 1904
|Contact| |Front page| |Contents| |Pythagorean Theorem|
Copyright © 1996-2018 Alexander Bogomolny73580913
