Pythagorean Theorem

J. Grossman

The following proof of the Pythagorean theorem using trigonometry was discovered (or is the proper word invented?) by David Houston, an eighth-grade student from Sterling Heights, Michigan, who comes to Oakland University to take mathematics courses and to chat with some of our faculty members on a regular basis. Bright students in a trigonometry class or a geometry class should be able to follow it.

If we define sinθ for any acute angle θ as the ratio of the opposite side to the hypotenuse in a right triangle with angle θ, then the area formula A = xy sinθ / 2 follows from the formula A = bh / 2, as shown in the following diagram (AB: bh here is a shorthand for "base times altitude.")

To establish the Pythagorean theorem, we want to prove that a² + b² = c² in the following diagram.

Without loss of generality, we assume that a ≤ b; in what follows, we ignore the case a = b (which guarantees that θ is acute), but it is easy to modify the argument to handle that special case.

In the figure on the left, we see that on the one hand, the total area is 2·ab / 2 = ab, whereas by the trigonometric area formula, it is also c² sinθ / 2. Therefore,

ab = c² sinθ / 2.

The figure on the right is formed by reflecting the original triangle about the line through the right-angle vertex, parallel to the hypotenuse. Since each copy of the right triangle clearly occupies half of its half of the large rectangle, the total area is 2ab. On the other hand, if we add the areas of the four triangles in this figure, we see that the area ab (from the two copies of the original right triangle) plus b² sinθ / 2 (from the triangle on the right - the marked angle is θ, since it is twice the included angle between b and c by the alternate-interior-angle property) plus a² sinθ / 2 (from the triangle on the left - the included angle between the a sides is the supplement of θ). Equating these two quantities, we have

ab = (a² + b²) sinθ / 2.

The Pythagorean formula then follows immediately from the two displayed equations.

Comment

As I mentioned in the introduction to the Pythagorean theorem page, E. Loomis expressed an opinion that the Pythagorean theorem does not admit a trigonometric proof. That opinion is no doubt shared by the majority of mathematicians. The reason for this is the fact that cos²α + sin²α = 1 is one of the most basic trigonometric identities, with the implication that using trigonometry to prove the Pythagorean proposition would entail a vicious circle. The Pythagorean theorem is so fundamental to the development of trigonometry that, e.g., I. M. Gelfand and M. Saul in their book Trigonometry found it necessary to supply several proofs of the theorem in Chapter 0, naturally preceding all the rest of the book.

The definitions of trigonometric functions are based on the theory of proportion and similarity. For example, all right triangles with the same angle α are similar and, for similar triangles, the ratios of two corresponding sides are equal; in particular, the ratio of a leg to the hypotenuse is a function of the adjacent (or the opposite) acute angle. For the adjacent angle the function is called cosine, for the opposite angle it is called sine. As long as a proof of the Pythagorean identity contains only the definitions of trigonometric functions, one may reasonably claim that the use of trigonometry is entirely spurious. The functions can be simply replaced by the ratios, leading to a plain algebraic proof. A remark to this effect has been made at the end of Proof #6.

David Houston's proof makes use of trigonometry twice. First, the proof depends on the trigonometric formula for the area of a triangle A = xy sinθ / 2. Second, later on the proof utilizes a property of sine which asserts that the sines of supplementary angles are equal: sinα = sin(π - α). (In [Gelfand & Saul, p. 71] this is true simply by definition.)

We might have proceeded as follows.

The theory of similarity and proportion allows us to make an observation: let x, y be the sides of a triangle with the included angle θ. Let h be the length of the altitude to side x. Then the ratio h/y is the function of (depends only on) angle θ. Let's denote this function as F: h/y = F(θ).

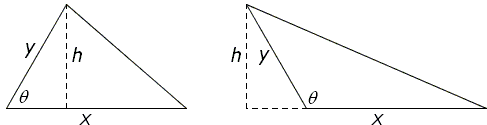
The above diagram implies F(θ) = F(π - θ). By definition, h = yF(θ) which leads to a formula for the area of a triangle S: S = xy F(θ) / 2. In the case of an isosceles triangle with x = y, the formula gives S = x² F(θ) / 2. David Houston's proof may take off form this point. It is not at all important that originally a trigonometric function made an appearance in the proof. This just threw a veil over its dependency on more fundamental properties of similar figures. It is worth comparing David's proof with a variant of VI.31:

David's configuration is obtained by reflecting the above in the lowest orange line. The argument that also employs similarity of triangles, proportions and areas could be extended to David's configuration.

However, David's argument is different and, to boot, the trigonometric formula for the area of a triangle plays such a prominent role in the proof that replacing sine with an auxiliary function F seems (to me at least) a rather artificial device. In a hindsight, one was indeed able to do away with trigonometry thus confirming Loomis' view. On the other hand, there are grounds for a reasonable doubt whether anybody without the knowledge of trigonometry would have been able to come up with such a nice and simple proof as David's.

Note: Luc Gheysens came up with a modification of David Houston's proof that leads to a shorter derivation.

References

I. M. Gelfand, M. Saul, Trigonometry, Birkhäuser, 2001
J. Grossman, a reader's letter in Mathematics Teacher, v. 87, n. 1, January 1994, NCTM
E. S. Loomis, The Pythagorean Proposition, NCTM, 1968

71921476