Pythagorean Theorem

Proof by Luc Gheysens

The proof of the Pythagorean theorem discussed below makes employs the sin formula for the area of the triangle and, thus, appears to use trigonometry in an essential way. The proof is due to Luc Gheysens from Flanders (Belgium). As Luc has observed, the proof is a shortened variant of Proof #80.

Combine two copies of the same right triangle in two ways as shown in the diagrams below:

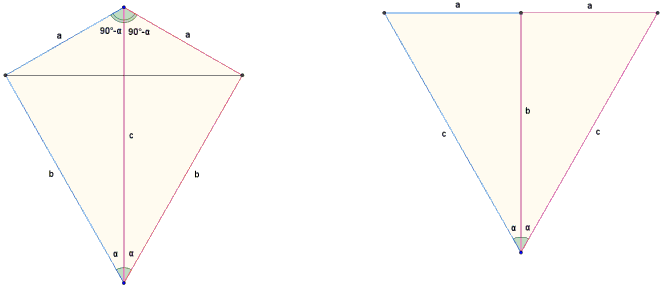
When joined at the hypotenuse, the triangles form a kite that can be seen as a union of two isosceles triangle, with the area of

b²sin(2α)/2 + a²sin(180° - 2α)/2 = (a² + b²)·sin(2α)/2.

When joined at one of the legs (b in the right diagram), the triangles form an isosceles triangle with base 2a and the sides equal to c. Applying the same area formula to that triangle we obtain

c²sin(2α)/2 = (a² + b²)·sin(2α)/2

and the Pythagorean theorem follows.

Remark: The configurations on which the proof is based allow for another derivation based on Heron's formula as was done in Proof #75.

The area of the kite is obviously ab and its square a²b². The isosceles triangle in the right diagram has the semiperimeter equal to a + c. Heron's formula applied to that triangle leads to

a²b² = (c + a)(c - a)a² = (c² - a²)bc²,

which implies the Pythagorean theorem.

71753346