Same Configuration - Several Proofs

Twice in his proof of I.47 Euclid used the fact that if a parallelogram and a triangle share the same base and are in the same parallels (I.41), the area of the parallelogram is twice that of the triangle. Wondering at the complexity of the setup that Euclid used to employ that argument, Douglas Rogers came up with a significant simplification that Euclid without a doubt would prefer if he saw it.

Let ABA'B', ACB''C', and BCA''C'' be the squares constructed on the hypotenuse and the legs of ΔABC as in the diagram below. As we saw in proof 63, B' lies on C'B'' and A' on A''C''. Consider triangles BCA' and ACB'. On one hand, one shares the base BC and is in the same parallels as the parallelogram (a square actually) BCA''C''. The other shares the base AC and is in the same parallels as the parallelogram ACB''C'. It thus follows by Euclid's argument that the total area of the two triangles equals half the sum of the areas of the two squares. Note that the squares are those constructed on the legs of ΔABC.

On the other hand, let MM' pass through C parallel to AB' and A'B. Then the same triangles BCA' and ACB' share the base and are in the same parallels as parallelograms (actually rectangles) MBA'M'and AMM'B', respectively. Again employing Euclid's argument, the area of the triangles is half that of the rectangles, or half that of the square ABA'B'. And we are done.

As a matter of fact, this is one of the family of 8 proofs inserted by J. Casey in his edition of Euclid's Elements. I placed the details on a separate page.

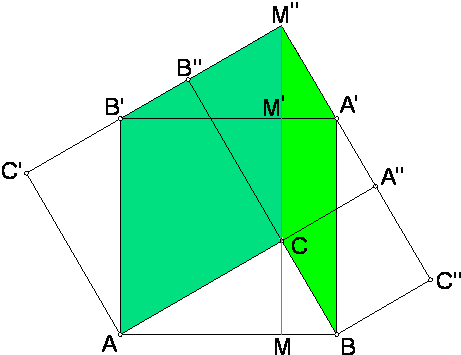
Now, it appears that the argument can be simplified even further by appealing to the more basic (I.35): Parallelograms which are on the same base and in the same parallels equal one another. The side lines C'B'' and A'C'' meet at point M'' that lies on MM', see, e.g. proof 12 and proof 24. Then by (I.35) parallelograms AMM'B', ACM''B' and ACB''C' have equal areas and so do parallelograms MBA'M', BA'M''C, and BC''A''C. Just what is needed.

The latter approach reminds one of proof 37, but does not require any rotation and does the shearing "in place". The dynamic version and the unfolded variant of this proof appear on separate pages.

In a private correspondence, Kevin "Starfox" Arima pointed out that sliding triangles is a more intuitive operation than shearing. Moreover, a proof based on a rearrangement of pieces can be performed with paper and scissors, while those that require shearing are confined to drawings or depend on programming, e.g. in Java. His argument can be represented by the following variant of both this proof and # 24.

A dynamic illustration is also available.

Rotatating the diagram for convenience helps make a transparent algebraic argument found by Michaelangelo Lucas. There are two ways to eveluate the area of the composite body.

On one hand, the shape consists of three right triangles with sides a, b, c and combined area of 3ab/2, and of square c². On the other hand, the shape is the union of a rectangle b×(a+b) and a trapezoid with height a and two bases a and (a+b), the latter having the area a(2a+b)/2.

Computing the area of the same figure in two ways leads to an equation

3ab/2 + c² = b(a + b) + a(2a + b)/2.

Simplifying we obtain the Pythagorean identity. (Of couse, it is also possible to interpret the diagram more in line with another famouse proof and see as consisting of two squares a² and b² and three (add-on) triangle with area ab/2.

Michaelangelo originally came up with a symmetric, more eye-pleasing configuration.

Derivation practically remains the same.

71545255