J. Casey's Additions to Euclid I.47

Maciej Maderek from Poland has advised me of a popular Polish book, Sladami Pitagorasa by Szczepan Jelenski published in 1988. Among several proofs of the Pythagorean theorem Jelenski lists 8 with common characteristics:

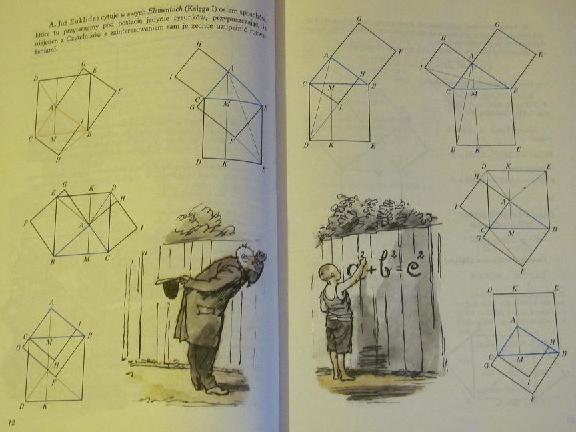
Maciej found out that the 8 proofs have been mentioned in J. Casey's 1885 edition of Euclid's Elements. Following Euclid's proof of I.47, Casey wrote:

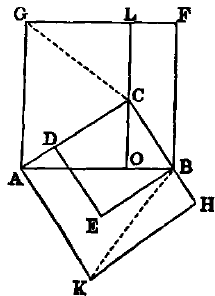Or thus: Let all the squares be made in reversed directions. Join CG, BK, and through C draw OL parallel to AG. Now, taking the ∠BAC from the right ∠s BAG, CAK, the remaining ∠s CAG, BAK are equal. Hence the Δs CAG, BAK have the side CA = AK, and AG = AB, and the ∠ CAG = BAK; therefore [IV.] they are equal; and since [XLI.] the rectangles AL, AH are respectively the doubles of these triangles, they are equal. In like manner the rectangles BL, BD are equal; hence the whole square AF is equal to the sum of the two squares AH, BD.

This proof is shorter than the usual one, since it is not necessary to prove that AC, CD are in one right line. In a similar way the Proposition may be proved by taking any of the eight figures formed by turning the squares in all possible directions. Another simplification of the proof would be got by considering that the point A is such that one of the Δs CAG, BAK can be turned round it in its own plane until it coincides with the other; and hence that they are congruent.

The sketch for this proof appears in the lower right cornercorner of Jelenski's page above. One of this, viz., the middle sketch on the left, is a clear illustration of Proof 69 in our collection. This latter is also listed by Loomis, as the geometric proof #84. Another variant, with the square on one leg drawn internally and on the other externally is Loomis' #128 and is claimed to be original with the author (August 1, 1990.) Loomis' proof #77 is identical to his #84, with credits to Versluys (1914), Wipper (1895, 1897), and Peter Warins (1762).

Loomis mentions neither Casey nor the relationship between the eight proofs the latter observed.

References

1. E. S. Loomis, The Pythagorean Proposition, NCTM, 1968

|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry| |Store|