Pythagorean Theorem through Angles 60 and 120
The proof below is due to Burkard Polster and Marty Ross and is a part of their refreshing paper in the Mathematics Magazine (VOL. 89, NO. 1, FEBRUARY 2016 47-54.) It employs their discovery of proofs of the Law of Cosines for triangles with angles of $60^{\circ}\;$ and $120^{\circ},\;$ the proofs that depend on neither the Pythagorean theorem nor on the general Law of Cosines. In this the proof is reminiscent of the one by Floor van Lamoen which derived the general statement of the Pythagorean theorem from the case of the right isosceles triangle.
The proof is based on the following diagram:
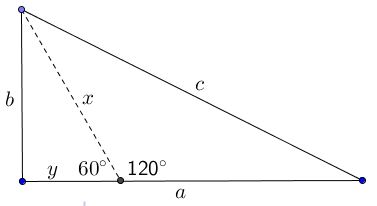
Any right triangle can be split into one with angle $60^{\circ}\;$ and another with angle of $120^{\circ}.\;$ Using the notations in the diagram and with the reference to Polster & Ross's result, we can write.
$c^2=x^2+(a-y)^2+x(a-y),\\ b^2=x^2+y^2-xy.$
Now subtracting the second one from the other gives $c^2-b^2=a^2+a(x-2y).\;$ But obviously $x=2y:$
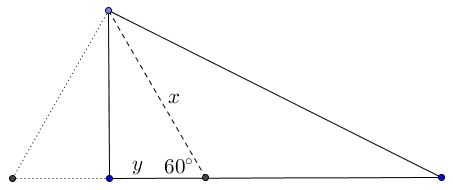
Thus, we arrive at the Pythagorean identity $c^2-b^2=a^2.$
|Pythagorean Theorem| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581861
