Each of the given 9 lines cuts a given square into two quadrilaterals whose areas are in proportion 2:3. Prove that at least three of these lines pass through the same point.

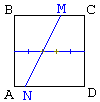
None of the given lines may pass through two successive sides of the square because then we'd get a triangle and a pentagon and not two quadrilaterals. Assume one of them intersects sides BC and AD at points M and N, respectively. The quadrilaterals, ABMN and CDNM, are both trapezoids with equal heights. Therefore, their areas are in the same ratio as their midlines. From here, MN intersects the midline of the square in ratio 2:3!. This is true for any one of the nine lines. But there are only four points that divide the midlines of the square in the ratio 2:3. Therefore, by the Pigeonhole Principle, at least three of the lines pass through the same point.