Square, 45 Degrees Angle and Pythagoras' Look-alike
What Is It About?
Problem
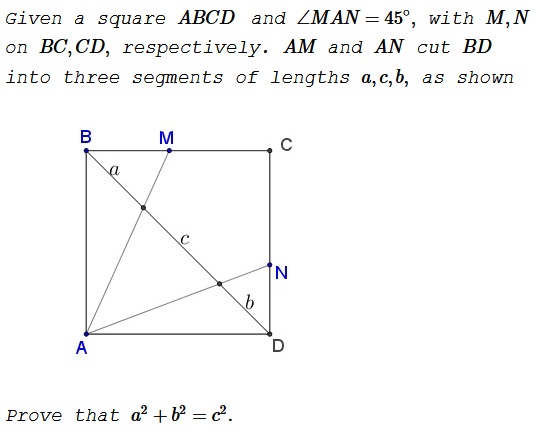
Solution 1
Rotate the square around $A$ through $90^{\circ}$ counterclockwise. Then $BD$ maps onto $B'B$ which means that $\angle B'BD=90^{\circ}.$
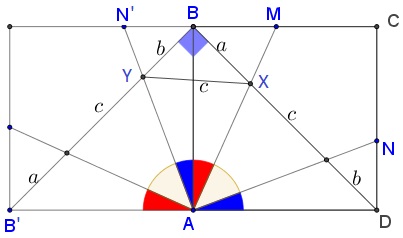
If $N$ maps onto $N'$ then
$\displaystyle \begin{align} \angle MAN' &= \angle MAB+\angle BAN'= \angle MAB+\angle DAN\\ &=90^{\circ}-\angle MAN=45^{\circ}. \end{align}$
If $X,Y,y'$ are as in the above diagram, then $AY=AY'$ and $\Delta AXY'=\Delta AXY$ so that $XY'=c.\,$ Thus $\Delta XBY'$ is right at $B$ with legs $a,b$ and hypotenuse $c.$ A reference to the Pythagorean theorem completes the proof.
Solution 2
Now by paper folding:
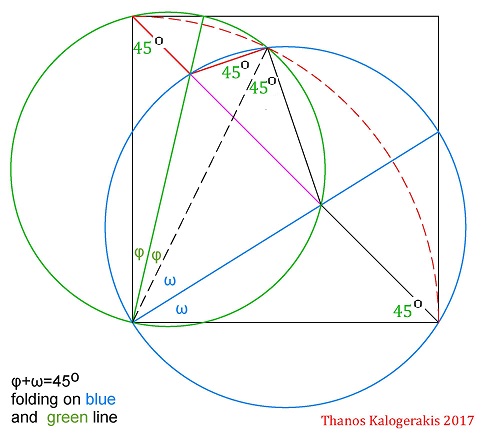
Solution 3
Let the diagonals of the square intersect in point $X$ and $\angle MAX=\phi.$ WLOG, let the diagonal of the square be $2.$ Thus,
$\displaystyle a= 1-\tan\phi,~\text{and}~b= 1-\tan\left(\frac{\pi}{4}-\phi\right).$
$\displaystyle \tan\left(\frac{\pi}{4}-\phi\right)=\frac{1-\tan\phi}{1+\tan\phi} \Rightarrow 1-b=\frac{1-(1-a)}{1+(1-a)}=\frac{a}{2-a}.$
$ c^2-a^2-b^2=(2-a-b)^2-a^2-b^2=2[(2-a)(1-b)-a]=0.$
Acknowledgment
The problem was posted by Deepak Kumar at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group. Solutions 1 and 2 are by Thanos Kalogerakis; Solution 3 is by Amit Itagi.
There is a problem that is solved by the same rotation - swiveling around one of the corners of the square through $90^{\circ},$ Point in a square, and another one, solved by a rotation through $60^{\circ},$ Equilateral and 3-4-5 Triangles.
|Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2018 Alexander Bogomolny73570844
