A Problem with Two Similar Rectangles
What Is This About?
Created with GeoGebra
Source
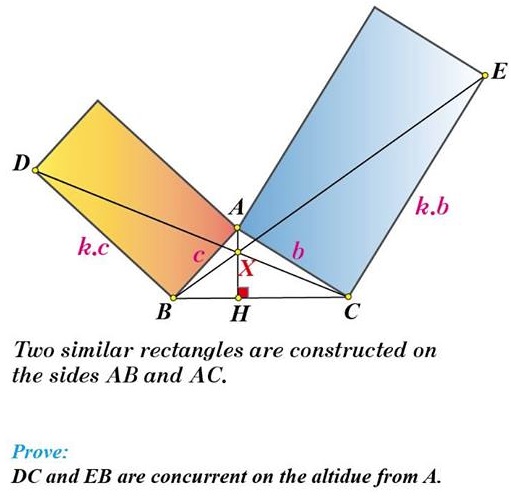
Solution 1
Using complex numbers, let $A=i,\,$ $B=-u,\,$ $C=v,\,$ with $u=\cot B\,$ and $v=\cot C.\,$ We have $\displaystyle \frac{E-C}{A-C}=-ki,\,$ implying $E=c+k+cki.\,$ Similarly, $D=-b-k+bki.\,$ From Here, $BE\,$ is defined by $-ckx+(b+c+k)y=bck\,$ and $CD\,$ by $BKX+(b+c+k)y=bck.\,$ Since $AH,\,$ the altitude, is defined by $x=0,\,$ suffice it to show that
$\left|\begin{array}{ccc}\,1&0&0\\-ck&b+c+k&bck\\bk&b+c+k&bck\end{array}\right|=0,$
which is obvious.
Solution 2
Let $h=AH.\,$ Then $BH=\sqrt{c^2-h^2}\,$ and $CH=\sqrt{b^2-h^2}.\,$ Drop a perpendicular from $E\,$ to $BC.\,$ BY $AAA\,$ test, triangles $AHC\,$ and $CFE\,$ are similar. Thus $EF=k\sqrt{b^2-h^2}\,$ and $CF=kh.$
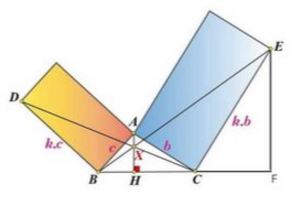
Triangles $BHX\,$ and $BFE\,$ are similar. Thus,
$\displaystyle HX=\frac{EF\cdot BH}{BF}=\frac{k\sqrt{b^2-h^2}\sqrt{c^2-h^2}}{kh+\sqrt{b^2-h^2}+\sqrt{c^2-h^2}}.$
This expression was derived using the blue rectangle and is completely symmetric in $b\,$ and $c.\,$ Thus, a similarly derived expression using the orange rectangle results in the same expression. Hence, $BE\,$ and $CD\,$ intersect $AH\,$ at the same point.
Solution 3
The problem strongly reminds of what is known as Vecten's configuration, with the difference that squares on the sides of a triangle have been replaced with similar rectangles. The configuration has many interesting properties. The proof of the one at hand is practically the same as before (see F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991, p 225).
Drop perpendiculars from $B\,$ and $C\,$ to $CD\,$ and $BE,\,$ respectively.Let $K\,$ and $L\,$ be the points of intersection. We'll prove that $BK\,$ and $CL\,$ meet on the extension of $AH.\,$ If that point is denoted $J,\,$ then this will make $BK,\,$ $CL\,$ and $AH\,$ the altitudes in $\Delta BCJ,\,$ from which the required statement follows immediately.
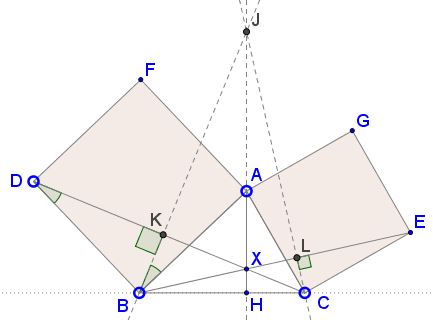
To start with, let $J\,$ be the intersection of $BK\,$ and $AH.\,$ Consider triangles $BCD\,$ and $ABJ.\,$ By simple angle chasing, $\angle BDC=\angle ABJ\,$ and $\angle CBD=\angle BAJ.\,$ Thus the two triangles are similar; in particular,
$\displaystyle AJ=BC\cdot\frac{AB}{BD}=BC\cdot\frac{AC}{CE},$
due to the similarity of the rectangles. This means that $J\,$ also serves as the intersection of $CL\,$ and $AH.\,$ The proof is complete.
Solution 4
The statement is a direct consequences of Jacobi's theorem:
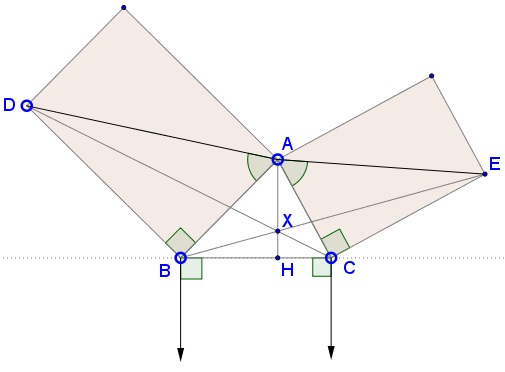
An Extension of Friendship
In 2001, Floor van Lamoen has introduced the notion of friendship among triangle centers. In particular, in Vecten configuration, the extension of the altitude through the common vertex of $\Delta ABC\,$ is the median in $\Delta AGF,\,$ which is one of the flank triangles. This property also holds for the present configuration:
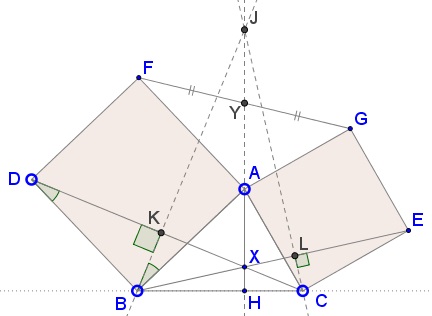
This is left as an exercise.
Acknowledgment
The problem by Kadir Altintas has been kindly posted by Leo Giugiuc at the CutTheKnotMath facebook page, along with his solution (Solution 1). Solution 2 is by Amit Itagi; Solution 4 is by Daniel Liu and, independently, by Kostas Vittas.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73562206
