Two Equilateral Triangles on Sides of a Square

Problem

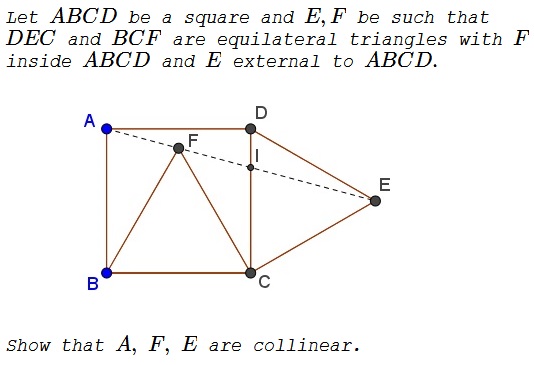
Two Equilateral Triangles on Sides of a Square, problem

Solution 1

Consider the counterclockwise rotation $r$ around $C$ through $60^{\circ}.$ $r(E)=D,$ $r(F)=B,$ and let $r(A)=A'.$ Then $\Delta AA'C$ is equilateral. In particular, $AA'=CA'.$ It follows that $AA'CD$ is a kite so that $A'D$ is the perpendicular bisector of $AC.$ But so is $BD,$ making $A',B,D$ collinear.

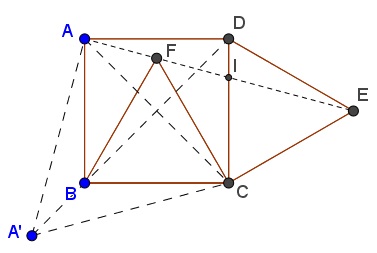
Two Equilateral Triangles on Sides of a square, proof

Rotations conserve collinearity, so that $A=r^{-1}(A'),$ $F=r^{-1}(B),$ and $E=r^{-1}(D)$ are collinear.

Illustration to Solution 1

Two Equilateral Triangles on Sides of a square, solution 1, illustration

Solution 2

$\displaystyle \frac{1}{2}\div\frac{1-\sqrt{3}}{2}=\frac{1+\sqrt{3}}{2}\div\frac{1}{2}$ with $K$ midpoint of $AD$ and $I$ extension of $AD$ such that $\angle AIE=90^{\circ}.$ Thus $\displaystyle \frac{AK}{KF}=\frac{AI}{IE}.$

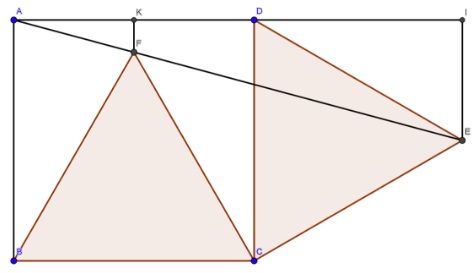
Two Equilateral Triangles on Sides of a square, solution 2

Therefore $A,F,E$ are collinear.

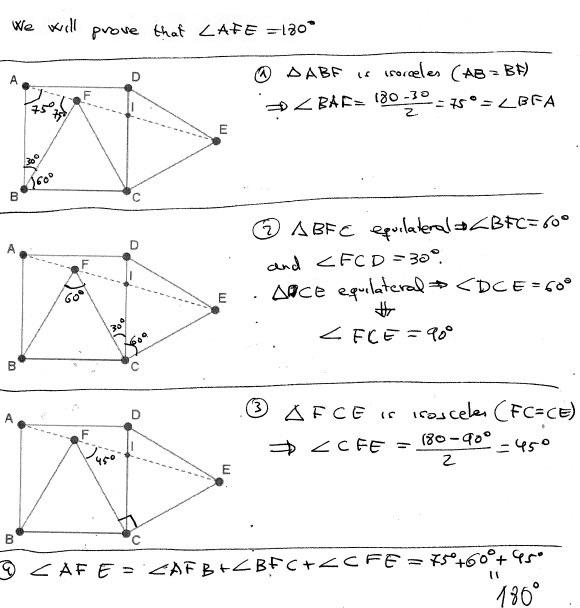
Solution 3

Angles of $\Delta AFB$ are $75-75-30,$ so the $\angle AFB=75^{\circ}.$ $\angle ADE=15^{\circ}$ and $|AD|=|DE|$ so that $\angle DEA = 15^{\circ},$ making $\angle AEC = 45^{\circ}$ and, in turn, $\angle CFE = 45^{\circ}.$ $\angle AFB + \angle BFC + \angle CFE = 180^{\circ},$ therefore $A,$ $F,$ and $E$ are collinear.

Solution 4

Assume $+X$ axis along $AB$ and $+Y$ axis along $AD$. WLOG, let the side of the square be of unit length. Let $s=\sin\angle FBC$ and $c=\cos\angle FBC$.

$\begin{align} \vec{AF}&=(1-s)\hat{x}+c\hat{y} , \\ \vec{AE}&=c\hat{x}+(1+s)\hat{y}, \\ |\vec{AF}\times\vec{AE}|&=|(1-s)(1+s)-c^2|=|1-(s^2+c^2)|=0. \end{align}$

Note, I have not used $60^{\circ}$ anywhere. Thus, this proof can be generalized to the following case:

$BF=DE=AB$ and $\angle FBC=\angle EDC$.

The equilateral triangle condition is not necessary.

Solution 5

Two Equilateral Triangles on Sides of a square, solution 5

Solution 6

(Solved with rational trigonometry.)

Let the quadrance of $AB = Q.$ Then the spread between $BF$ and $BC$ is $\displaystyle \frac{3}{4}$ by the cross law. Then the $\displaystyle s(BA, BF) = \frac{1}{4} = s(AD, DE)$ by sum of spreads in right triangle. By cross law $Q(AF) = Q\cdot (2-\sqrt{3})$ and $Q(AE) = Q(2+\sqrt{3}),$ and $Q(FE) =2.$

$Q(AF),$ $Q(AE),$ $Q(FE)$ form a quad triple, therefore $A, E, F$ are collinear.

Some ambiguity: I denoted the quadrance of a side by $Q,$ and also use $Q(\text{segment})$ to denote the quadrance of that segment.

For reference

Two Equilateral Triangles on Sides of a square, solution 6, references

Solution 7

Take coordinates of square as $A(0,0),$ $B(1,0),$ $C(1,1),$ $D(0,1).$ Then, $F$ is $\displaystyle \left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)$ and $\displaystyle E\left(1+\frac{\sqrt{3}}{2},\frac{1}{2}\right).$ Area of $\Delta DFE$ equals $0.$ Hence, the three points are collinear.

Acknowledgment

The problem (and the solution) come from Michel Bataille's column "FOCUS ON..." in the Canadian Crux Mathematicorum (v 44, n 1, pp 25-27). Solution 2 is by Marcos Carreira and Luca Moroni; Solution 3 is by Ibrahim Akalin; Solution 4 is by Amit Itagi; Solution 5 is by Calendari Matemàtic; Solution 6 is by HIGHOctane; Indiana Jones.

The illustration to Solution 1 is by Crawl.

71948539