A brief introduction to Rational Trigonometry
Greek approach to measurement
N. J. Wildberger
Euclid does not deal directly with distance. The ancient Greeks understood the meaning of saying two segments in the same direction were in the ratio `three to two', but they did not have a direct notion of distance, because that would have entailed an understanding of real numbers, which they did not have. Similarly, Euclid does not measure angle. To him, an angle was just the geometrical configuration consisting of two intersecting lines. In fact the modern notion of `radian measure' is only a little more than a hundred years old.
Instead of distance and angle, the ancient Greeks believed that area is the fundamental quantity in planar geometry. To measure the separation of two lines, they measured the area of a square built on that line segment, a process called quadrature. A new theory of trigonometry, called rational trigonometry, was developed in 2005 by N. J. Wildberger (UNSW) in Divine Proportions: Rational Trigonometry to Universal Geometry, Wild Egg Books, Sydney, 2005, https://wildegg.com. Downloads from the book, supporting articles and links to reviews are available at https://wildegg.com/authors/. This note briefly motivates this new approach and lists the main laws, which require no transcendental circular functions.
Pythagoras' theorem
There are two really important theorems about areas formed by three points.
One is well known, the other much less so. Proposition 47 of Book 1 of
Euclid's Elements states that for a right angled triangle, the
square on the hypotenuse is the sum of the squares on the
other two sides. This version of Pythagoras'
theorem uses area, not distance. Area is an affine concept, in the
sense that proportions between areas are invariant under affine
transformations, which include linear transformations. To measure a line
segment, Euclid measures the area of a square on that
segment, a number which we call quadrance, being close
to the word quadrature. If
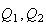 and
and
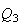 are the three quadrances of a right triangle
are the three quadrances of a right triangle
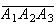 for which
for which
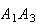 is perpendicular to
is perpendicular to
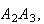 then Pythagoras' theorem can be stated
as
then Pythagoras' theorem can be stated
as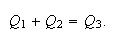 For
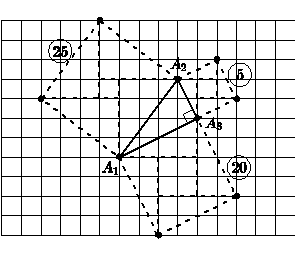
a triangle with rational points (vertices), the quadrances are rational
numbers which can be determined combinatorially---by counting cells in a
suitable grid lattice, as in the figure with
For
a triangle with rational points (vertices), the quadrances are rational
numbers which can be determined combinatorially---by counting cells in a
suitable grid lattice, as in the figure with
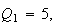
 and
and
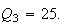
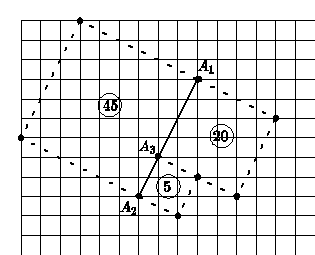
Triple quad formula
Pythagoras' theorem has a sister theorem that Euclid does not mention, but
which is implicit in work of Archimedes, and fundamental for rational
trigonometry. It concerns the case when the three points
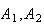 and
and
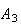 are collinear. In this case the three quadrances
satisfy the Triple quad formula
are collinear. In this case the three quadrances
satisfy the Triple quad formula
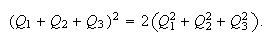
The figure shows a case where
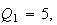
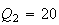 and
and
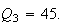
Although algebraically more complicated, the Triple quad formula is in some
sense a one-dimensional result, and easier to prove. Although Euclid did not
have this theorem, one could argue that Archimedes did, as it is closely related
to Herons' formula, known to Archimedes.
Main laws of rational trigonometry
An angle is a circular distance, that is distance
measured along a circular arc, and this is too
complicated a concept to qualify as fundamental for measuring the
separation of two lines. To define angles properly you require calculus, a
logical point that is rarely acknowledged by educators. Teachers of
trigonometry constantly rely on
The true separation between lines
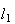 and
and
 is captured by the concept of spread, which may be
defined as the ratio of two quadrances. Suppose
is captured by the concept of spread, which may be
defined as the ratio of two quadrances. Suppose
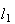 and
and
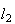 intersect at the point
intersect at the point
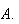 Choose a point
Choose a point
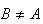 on one of the lines, say
on one of the lines, say
 and let
and let
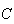 be the foot of the perpendicular from
be the foot of the perpendicular from
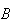 to
to
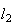 .
.
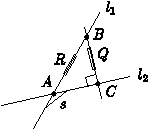
Then the spread s between l1 and l2 is
| s = s(l1, l2) = Q(B, C) / Q(A, B) = Q / R. |
is
ratio is clearly independent of the choice of
 by Thales' theorem. The spread is defined between lines, not rays. Parallel
lines are defined to have spread
by Thales' theorem. The spread is defined between lines, not rays. Parallel
lines are defined to have spread
When lines are expressed in Cartesian form, the spread becomes a rational
expression in the coefficients of the lines. It therefore makes sense over
arbitrary fields, although there is the possibility of null lines for which
the denominator involved in the spread is zero. Note that in the triangle
 above, the spread at the vertex
above, the spread at the vertex
 and the spread at the vertex
and the spread at the vertex
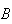 sum to
sum to
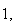 on account of Pythagoras' theorem.
on account of Pythagoras' theorem.
In diagrams a spread
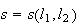 is displayed beside a small line segment joining the two lines to distinguish
it from angle. A spread protractor was created by
Michael Ossmann and is available online at
https://www.ossmann.com/protractor/.
is displayed beside a small line segment joining the two lines to distinguish
it from angle. A spread protractor was created by
Michael Ossmann and is available online at
https://www.ossmann.com/protractor/.
So now a triangle
 has quadrances
has quadrances
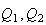 and
and
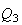 as well as spreads
as well as spreads
 and
and
 as in the following
diagram.
as in the following
diagram.
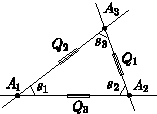
The other main laws of rational trigonometry are
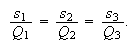 This
is the Spread law, the analog of the Sine law. The analog of
the Cosine law is the Cross law:
This
is the Spread law, the analog of the Sine law. The analog of
the Cosine law is the Cross law:
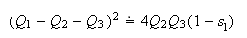
The relationship between the three spreads of the triangle is the
Triple spread law:
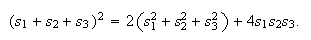
The Triple quad formula, Pythagoras'
theorem, the Spread law, the
Cross law and the Triple spread
formula are the five main laws of rational trigonometry. They are
implicitly contained in the geometrical work of the ancient Greeks. As
demonstrated at some length in `Divine Proportions',
these formulas and a few additional secondary ones suffice to solve the
majority of trigonometric problems, usually more simply, more accurately and
more elegantly than the classical theory involving
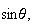
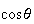 ,
,
 and their inverse functions. The same formulas extend to geometry over general
fields and with arbitrary quadratic forms. See supporting articles at https://wildegg.com/authors.htm.
and their inverse functions. The same formulas extend to geometry over general
fields and with arbitrary quadratic forms. See supporting articles at https://wildegg.com/authors.htm.
The triangle with vertices
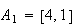 ,
,
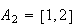 and
and
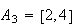 has quadrances
has quadrances
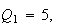
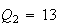 and
and
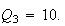 You can check that the spreads are
You can check that the spreads are
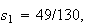
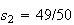 and
and
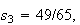 and verify directly that all the laws are satisfied.
and verify directly that all the laws are satisfied.
Since the laws are purely algebraic, they hold over a general field.
If we work over the field with
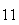 elements, the above triangle has quadrances
elements, the above triangle has quadrances
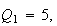
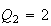 and
and
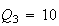 and spreads
and spreads
 ,
,
 and
and
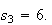 The above laws still hold.
The above laws still hold.
There is a collection of videos at YouTube that explains in detail the novel view point:
- WildTrig1: Why trig is hard
https://www.youtube.com/watch?v=ZYWHfvij94U - WildTrig2: Quadrance via Pythagoras and Archimedes
https://www.youtube.com/watch?v=3GU9mGyxz04 - WildTrig3: Spread, angles and astronomy
https://www.youtube.com/watch?v=9wd0i44vK04 - WildTrig4: Five main laws of rational trigonometry
https://www.youtube.com/watch?v=Oe2DZc6BXZk - WildTrig5: Applications of rational trigonometry
https://www.youtube.com/watch?v=BfqSln90zrA - WildTrig6: Heron's formula viewed rationally
https://www.youtube.com/watch?v=hooQuHLS-kk - WildTrig7: Solving triangles with rational trigonometry
https://www.youtube.com/watch?v=csprnzWN_lE - WildTrig8: Centers of triangles with rational trigonometry
https://www.youtube.com/watch?v=MIyPfv5Os6Y - WildTrig9: The laws of proportion for a triangle
https://www.youtube.com/watch?v=L9Xz3Es16wo - WildTrig10: Geometry of circles with rational trigonometry
https://www.youtube.com/watch?v=N7orImM4vsM - WildTrig11: Applications of rational trig to surveying (I)
https://www.youtube.com/watch?v=2Zd4931chJU - WildTrig12: Cartesian coordinates and geometry
https://www.youtube.com/watch?v=a6Pk-kbzhxA
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73598125
