A Problem with Three Equilateral Triangles
Source
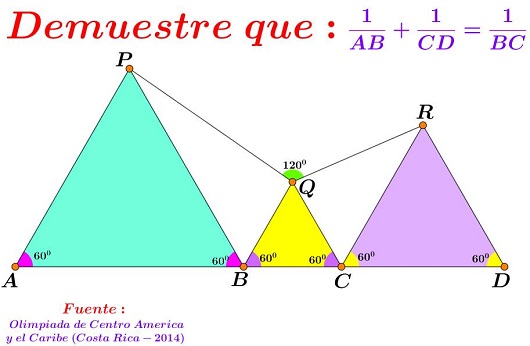
Solution 1
Extend $QR$ to $H$ on $AD,$ and, similarly, $PQ$ to $I.$
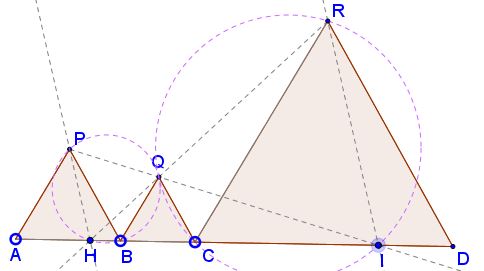
$\angle PQH=60^{\circ}=\angle PBH,$ making quadrilateral $BHPQ$ cyclic. Further, $\angle PHQ=\angle PBQ=60^{\circ}$ and, since $\angle PQH=60^{\circ},$ $\Delta PQH$ is equilateral. Similarly, $\Delta RQI$ is also equilateral.
Let's denote $AB=a,$ $BC=b,$ $CD=c.$ We need to show that $\displaystyle \frac{1}{a}+\frac{1}{c}=\frac{1}{b}.$ Also, for convenience, let $PQ=QH=u$ and $QR=QI=v.$ Triangles $\Delta HDR$ and $\Delta HCQ$ are similar as are $\Delta API$ and $\Delta BQI.$ It follows that
$\displaystyle\begin{align} &\frac{c}{b}=\frac{HR}{HQ}=\frac{v+u}{u}, &\;& \frac{a}{b}=\frac{PI}{QI}=\frac{u+v}{v},\\ &\frac{c-b}{b}=\frac{v}{u}, &\;& \frac{a-b}{b}=\frac{u}{v},\\ &\frac{c-b}{b}=\frac{b}{a-b}. \end{align}$
The latter simplifies to $ac=b(a+c),$ and further to the desired $\displaystyle \frac{1}{a}+\frac{1}{c}=\frac{1}{b}.$
Solution 2
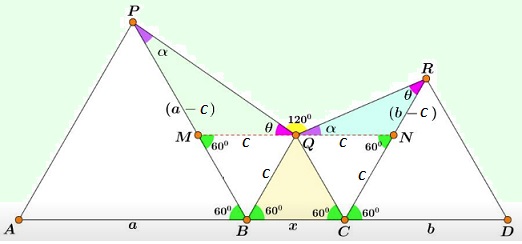
More directly, triangles $MQP$ and $QNR$ are similar so that $\displaystyle \frac{c}{a-c}=\frac{b-c}{c},$ from which $\displaystyle \frac{1}{a}+\frac{1}{c}=\frac{1}{b}.$
Solution 3
Let $AB=PB=x$, $CD=CR=y$, $BC=QB=QC=z$, and $\angle CRQ=\phi$. Hence, $\angle RQC=120^{\circ}-\phi$, $\angle PQB=60^{\circ}+\phi$, $\angle BPQ=60^{\circ}-\phi$.
Applying sine rule to $\Delta PQB$ and $\Delta RCQ$,
$\displaystyle\begin{align} \frac{x}{\sin(60^{\circ}+\phi)}&=\frac{z}{\sin(60^{\circ}-\phi)} \\ \frac{y}{\sin(120^{\circ}-\phi)}&=\frac{y}{\sin(60^{\circ}+\phi)}\\ &=\frac{z}{\sin\phi}. \end{align}$
Dividing the product of the two equations by the sum,
$\displaystyle \begin{align} \frac{xy}{x+y}&= z\frac{\sin(60^{\circ}+\phi)}{\sin\phi+\sin(60^{\circ}-\phi)} \\ &= z \frac{ \frac{\sqrt{3}}{2} \cos\phi + \frac{1}{2} \sin\phi }{ \sin\phi + \frac{\sqrt{3}}{2} \cos\phi - \frac{1}{2} \sin\phi} = z. \end{align}$
Thus,
$\displaystyle \frac{1}{z}=\frac{1}{x}+\frac{1}{y}.$
Extra
Quadrilateral $BCRP$ is tangential (inscriptible):
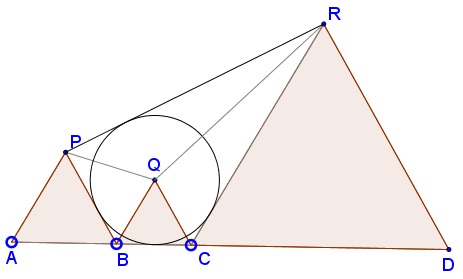
Applying the Law of Cosines three times:
$\begin{align}PQ^2&=a^2+b^2-ab\\ QR^2&=b^2+c^2-bc\\ PR^2&=PQ^2+QR^2+PQ\cdot QR. \end{align}$
Combining we get:
$PR^2=a^2+2b^2+c^2-ab-bc+\sqrt{(a^2+b^2-ab)(b^2+c^2-bc)}.$
Now, $BCRP$ is tangential iff $BC+PR=BP+CR,$ i.e., $PR=a+c-b.$ Thus we need to prove that
$(a+c-b)^2-a^2-2b^2-c^2+ab+bc=\sqrt{(a^2+b^2-ab)(b^2+c^2-bc)}$
or,
$2ac-b^2-ab-bc=\sqrt{(a^2+b^2-ab)(b^2+c^2-bc)}$
Squaring simplifies (thanks to wolframalpha) to $3(ac-b^2)(ac-ab-bc)=0,$ which, as we know, is correct.
Acknowledgment
The problem has been posted by Miguel Ochoa Sanchez at the Peru Geometrico facebook group. The problem was earlier offered at the 2014 Central American Mathematical Olympiad.
Solution 2 is by Miguel Ocho Sanchez and, independently, by Jesús Iván Herrera López; Solution 3 is by Amit Itagi.
The Extra is due to Thanos Kalogerakis' observation. More solutions can be found in comments at the Peru Geometrico facebook group.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73518717
