Triangular Areas in Circle
What is this about?
Problem
$A,$ $B,$ $C,$ $D$ are concyclic points on a circle $(O)$ and $AC$ perpendicular with $BD.$ Denote $[X]$ the area of $X.$
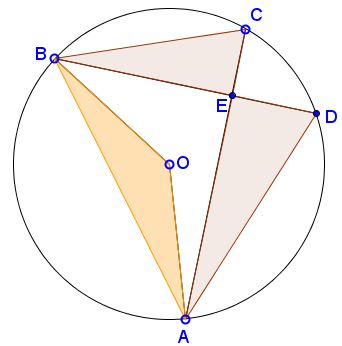
Prove that $\displaystyle\frac{[AED] + [BEC]}{2} = [AOB].$
Solution
Draw lines through $A$ and $C$ perpendicular to $AC,$ and through $B$ and $D$ perpendicular to $BD.$ These form a rectangle $IJKL$ which meets circle $(O)$ in four additional points, of which $F$ and $M$ are marked.
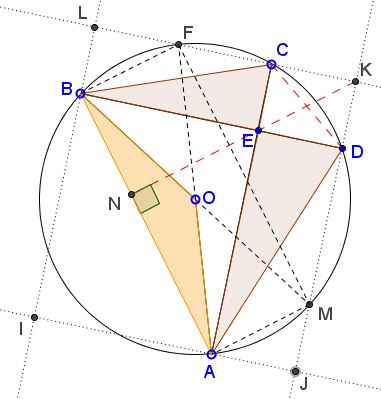
$\angle ACF=90^{\circ},$ hence $AF$ is a diameter of $(O);$ so is $BM.$ It follows that $ABFM$ is a rectangle and $[ABFM]=4[AOB].$
Now, due to the symmetry of the construction, $LF=AJ=ED$ and the three are parallel; also, $JM=BL=DK$ and the three are parallel, implying that the same can be said about $BF,$ $EK,$ and $AM.$ It follows that $BEKF$ and $AMKE$ are parallelograms. Furthermore, by Euclid I.34 and I.35,
$[BEKF]=[BECL]=2[BEC]$ and
$[AMKE]=[AJDE]=2[AED].$
Crucially, since $EK\parallel AM,$ $EK\perp AB.$ Let $N$ be the intersection of $EK$ with $AB:$ $EN\perp AB.$ It follows that $BN$ is the distance from $B$ to $EK.$ Therefore, $[BEKF]=EK\times BN;$ and similarly $[AMKE]=EK\times AN$ which shows that
$\begin{align} [BEKF]+[AMKE]&=EK\times BN+EK\times AN\\ &= EK\times AB\\ &= AM\times AB\\ &=[ABFM]. \end{align}$
Combining our findings we see that
$\begin{align} 2([BEC]+[AED])&=[BECL]+AJDE]\\ &=[ABFM]\\ &=4[AOB], \end{align}$
just as required.
Pythagorean theorem
It can be observed that triangles $AEB$ and, say, $CED$ (and the others, equal to $\Delta CED)$ are similar. This is because inscribed angles $BAC$ and $BDC$ are equal.

It follows that their sides are proportional. Let's introduce $a=BE,$ $b=AE,$ $c=AB,$ $x=CE,$ $y=ED,$ $z=CD.$ We then have $\displaystyle\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=r,$ for some $r\gt 0.$ What we have established above admits an algebraic interpretation:
$ax+by=cz.$
Substituting into this $x=ar,$ etc., leads to the Pythagorean identity.
Acknowledgment
The problem with solution has been posted by Bùi Quang Tuån at the CutTheKnotMath facebook page. An alternative solution can be found elsewhere. Bùi Quang Tuån has also suggested that the assertion of the problem implies the Pythagorean theorem.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579543
