Rectangular Areas in Circle

What is this about?

24 January 2015, Created with GeoGebra

Problem

Two rectangles, $ACDH$ and $BIFC,$ are drawn on the legs of right $\Delta ABC$ such that the points $A,B,F,D$ are concyclic. $DH$ meets circle $(ABFD)$ the second time in point $E,$ $FI$ in point $G.$

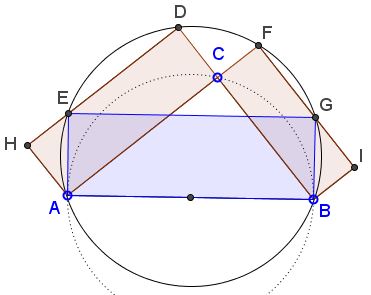
theree areas in circle - problem

Prove that $ABGE$ is a rectangle and $[ABGE]=[ACDH] + [BIFC],$ where $[X]$ denotes the area of shape $X.$

Solution

Since $\angle AFG=90^{\circ},$ $AG$ is a diameter of $(ABFD),$ making $\angle ABG$ right. Similarly, $\angle BAE=90^{\circ}.$ Because of the symmetry of chord embedding in a circle, this proves that $ABGE$ is a rectangle.$

theree areas in circle - problem

Let's introduce $a=BC,$ $b=AC,$ $c=AB,$ $x=CD,$ $y=CF,$ $z=AE.$ We have to prove that

(*)

$cz=ay+bx.$

There is a short algebraic derivation from the facts, implied in the diagram:

$a^{2}+b^{2}=c^{2},$ (Pythagorean theorem in $\Delta ABC.)$
$x^{2}+y^{2}=z^{2},$ (Pythagorean theorem in $\Delta AEH.)$
$ax=by.$ (Intersecting chords theorem.)

From here

$\begin{align} (cz)^{2} &= (a^{2}+b^{2})(x^{2}+y^{2})\\ &= (ax)^{2} + (ay)^{2} + (bx)^{2} + (by)^{2}\\ &= (ax)(by) + (ay)^{2} + (bx)^{2} + (ax)(by)\\ &= (ay)^{2} + 2(ay)(bx)+(bx)^{2}\\ &= (ay+bx)^{2}. \end{align}$

Since all quantities involved are positive, this proves (*).

Acknowledgment

The problem above is a reformulation of a cute problem posted by Bùi Quang Tuån at the CutTheKnotMath facebook page. Here's the original problem:

$A,$ $B,$ $C,$ $D$ are concyclic points on a circle $(O)$ and $AC$ perpendicular with $BD.$ Denote $[X]$ the area of $X.$

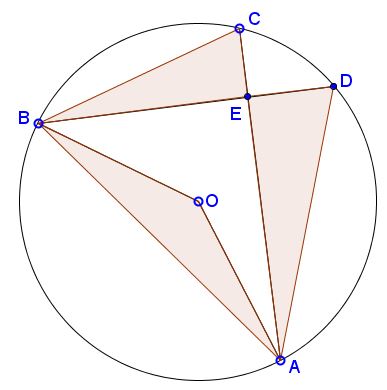
theree areas in circle - problem

Prove that $\displaystyle\frac{[AED] + [BEC]}{2} = [AOB].$

A synthetic solution of this problem can be found elsewhere.

71536354