A 60 degrees Rhombus in a 60 degrees Isosceles Trapezoid
What is this about?
A Mathematical Droodle
Created with GeoGebra, 24 November, 2016
Problem
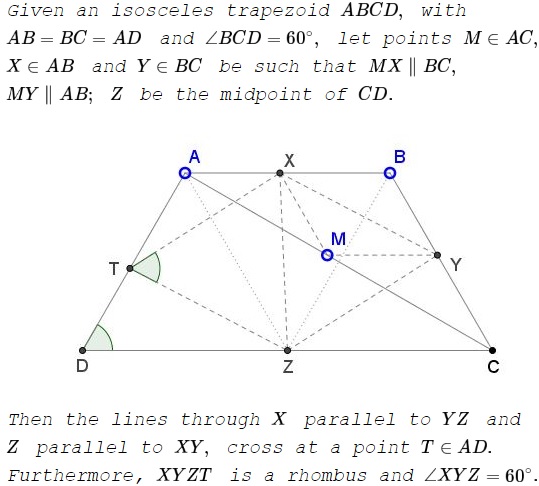
Proof
WLOG, assume $AB=BC=AD=1\;$ and denote $AX=x.\;$ Since $\Delta ABC\;$ is isosceles with base angles of $30^{\circ},\;$ so is $\Delta AXM,\;$ implying $XM=AX=x\;$ and, by the construction, $BY=x.\;$ By the Law of Cosines,
$\begin{align} XY^2 &= BX^2+BY^2-2BX\cdot BY\cos\angle XBY\\ &= (1-x)^2+x^2 + x(1-x)\\ &=x^2-x+1. \end{align}$
Let $T'\in AD\;$ be such that $DT=x.\;$ Then, as before, $T'X^2=x^2-x+1.\;$ in $\Delta DTZ,\;$ we have
$\begin{align} T'Z^2 &= DT'^2+DZ^2-2DT'\cdot DZ\cos\angle TDZ\\ &= x^2+1^2 - x. \end{align}$
Similarly, $YZ=x^2-x+1,\;$ such that $T'Z=TX=XY=YZ,\;$ showing that $XYZT'\;$ is a rhombus. In particular, $T'X\parallel YZ\;$ and $T'Z\parallel XY,\;$ making $T'=T.\;$ Now, in $\Delta AXZ,\;$ $AX=x=DT,\;$ $AZ=DZ=1,\;$ and $\angle XAZ=60^{\circ}=\angle TDZ.\;$ It follows that $\Delta AXZ=\Delta TDZ\;$ and, therefore, $XZ=TZ.\;$ This shows that $\Delta TXZ\;$ is equilateral and $\angle XYZ=\angle XTZ=60^{\circ}.$
Acknowledgment
Tran Quang Hung has kindly posted at the CutTheKnotMath facebook page a construction of the Golden Ratio in an isosceles trapezoid with an angle of $60^{\circ}.\;$ His construction, in part, reveals an inscribed rhombus with a $60^{\circ}\;$ angle. The above is a generalization that I think should be treated separately. The proof is a simple application of the Law of Cosines.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580715
