Symmedian in Right Triangle II

Ross Honsberger credits the simple proof below to John Rigby.

Let $AD\perp BC$ be the altitude to the hypotenuse in right $\Delta ABC.$ Triangles $ABC$ and $ABD$ (that share an angle at $B)$ are similar because also $\angle BAC=\angle ADB=90^{\circ}.$ The medians from the corresponding angles map onto each other. So letting $AM=CM$ and $AK=DK,$ we see that $\angle ABK=\angle CBM,$ implying that $BK$ is the symmedian in $\Delta ABC.$

In the same manner, similarity of triangles $ABC$ and $ACD$ shows that $CK$ is another symmedian in $\Delta ABC.$ Thus $K,$ as the intersection of two symmedians, is indeed the Lemoine point of $\Delta ABC.$

Note that, as a consequence, the altitude to the hypotenuse in a right triangle is simultaneously the symmedian from the right angle, as was discussed independently elsewhere.

References

1. R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995, 59-60

If, in $\Delta ABC,$ the Lemoine point $K$ coincides with the midpoint of the altitude $AD$ then $\angle BAC=90^{\circ}.$

Proof

Let, for a moment, $D$ on $BC$ be such that $\angle BDA=\angle BAC.$

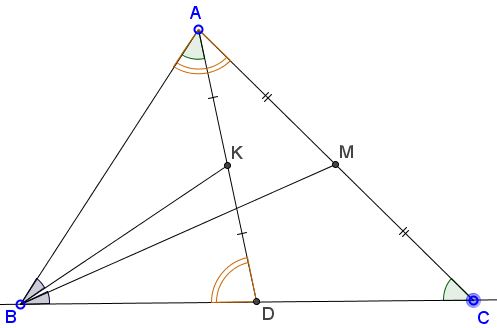
By the same argument as above, triangles $ABC$ and $ABD$ are similar, and the midpoint $K$ of $AD$ serves as the Lemoine point of $\Delta ABC.$ It follows that if $AD$ is the altitude from $A$ the angle $BAC$ (being equal to $\angle ADB)$ is right.

The characterization of right triangles discussed above and the reference to Ross Honsberger's book have been posted by Vladimir Nikolin at CutTheNotMath facebook page as a comment to another characterization of right triangles posted there.