A Characteristic Property Of Right Triangles

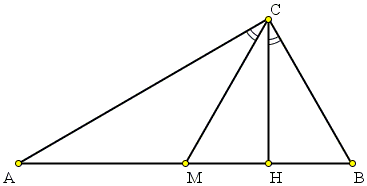
Let in ΔABC, CM is a median from C, CH is an altitude. Assume M != H. ∠ACB is right if and only if ∠ACM = ∠BCH.

a property of right triangles

I came across this property in an article Characterizations of Bicentric Quadrilaterals by Martin Josefsson (Forum Geometricorum, Volume 10 (2010) 165-173.) The proof below is different from that in the article.

Let in ΔABC, CM is a median from C, CH is an altitude. Assume M != H. ∠ACB is right if and only if ∠ACM = ∠BCH.

Proof

First assume that ∠ACB = 90°. Then AB is a diameter of the circumcircle. In particular, AM = CM, so that ΔACM is isosceles, implying ∠ACM = ∠CAM = ∠CAB.

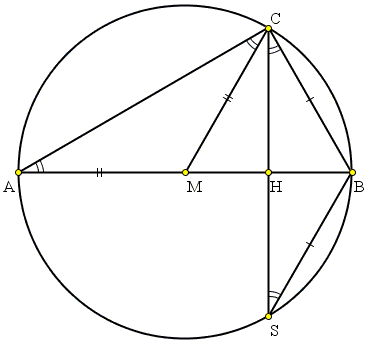
If S is the reflection of C in H then also ΔBCS is isosceles so that ∠BCH = ∠CSB. But angles CAB and CSB are inscribed and are subtended by the same arc, making them equal. Thus indeed ∠ACM = ∠BCH.

Conversely, assume ∠ACM = ∠BCH. Draw the angle bisector of angle ACB:

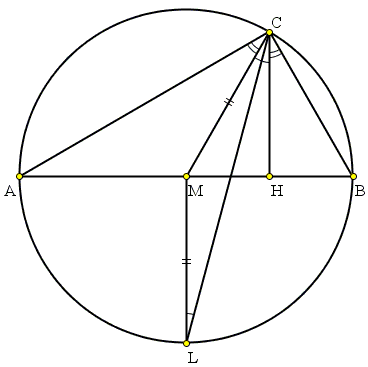
a property of right triangles, proof, step 2

The bisector intersects the circumcircle in L - the midpoint of arc AB - such that LM ⊥ AB. Since ∠ACM = ∠BCH and ∠ACL = ∠BCL, CL also bisects ∠MCH. On the other hand, CH||LM, implying ∠LCH = ∠CLM, as a vertical pair. In ΔCLM, ∠CLM = ∠MCL, making it isosceles, so that CM = LM. As the diagrams below illustrates, this is only possible when M is the circumcenter and AB a diameter of the circumcircle.

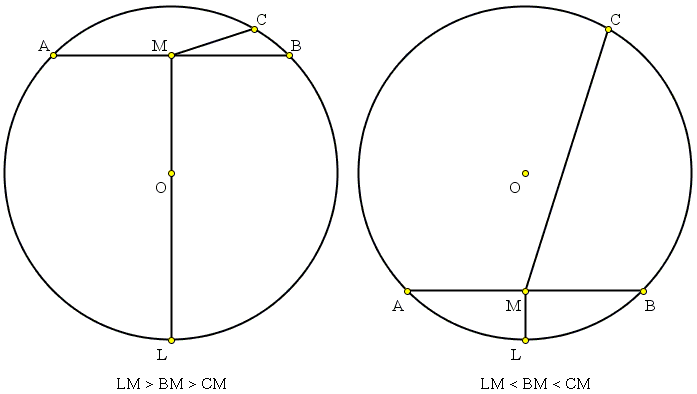
a property of right triangles, proof, step 4

Corollary

In the previous notations, ∠ACB is right iff its bisector also bisects ∠MCH.

41173670