A Straightedge Construction of the Midpoint of a Chord Common to Two Circles
What Is This About?
Problem
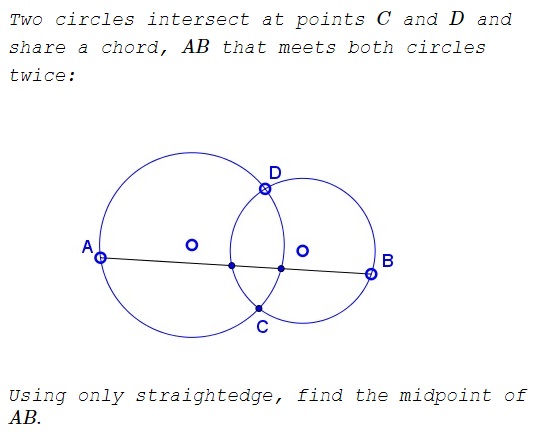
Solution
In the diagram below, $\angle \beta=\angle \gamma,$ as two inscribed angles subtended by the same chord $OL$ (not shown.) For the same reason, $\angle \gamma=\angle\delta,$ so that, by transitivity, $\angle \beta=\angle\delta.$
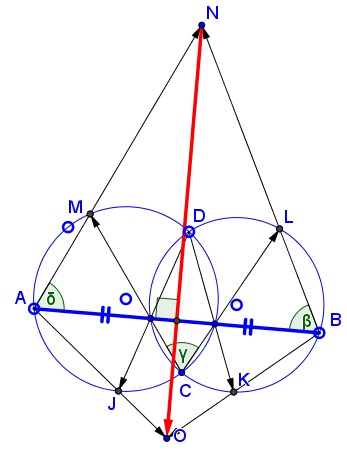
It follows that $AN=BN.$ Similarly, $AO=BO.$ It follows that $AOBN$ is a kite in which the diagonal $NO$ is perpendicular to the diagonal $AB$ and passes through the midpoint of the latter.
Acknowledgment
The problem is by Thanos Kalogerakis who kindly informed me of the problem and later communicated to me the solution by Nikoz Fragkakis.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73579852
