Spectral Decomposition of a Planar Quadrilateral: an Illustration

This is an illustration of the spectral decomposition of planar quadrilaterals described by Grégoire Nicollier elsewhere in the context of two recently published pages. The two pages dealt with the construction of similarly oriented squares on the sides of a quadrilateral and joining the midpoints of the segments between the pairs of adjacent vertices. The quadrilateral so obtained has been proved to possess special properties. In the general case of an arbitrary starting quadrilateral, the diagonals of the resulting quadrilateral are equal and perpendicular. If the starting quadrilateral is a parallelogram, the result is a square. The spectral decomposition described by Grégoire Nicollier leads to one line proofs of both results.

Planar quadrilaterals are vectors in $\mathbb{C}^4,\;$ whose (Fourier) basis consists of four quadrilaterals:

$F_0=(1,\,1,\,1,\,1),\quad F_1=(1,\,i,\,-1,\,-i) \text{ (positively oriented square)},\\ F_2=(1,\,-1,\,1,-\,1),\quad F_3=(1,\,-i,\,-1,\,i)=\overline{F_1} \text{ (negatively oriented square)}$

For example, the diagram below depicts the parallelogram

$(1-i)F_1+(2+i)F_3=(3,\,2-i,\,-3,\,-2+i)$

along with the squares constructed on its sides and the midpoints quadrilateral, which - in this case - is a square, as expected.

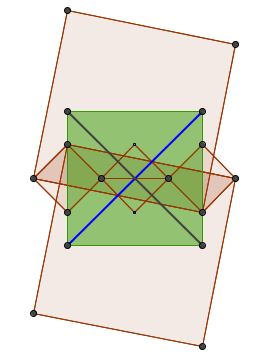
In the applet above, the sliders define the decomposition $(x_0+iy_0)F_0+(x_1+iy_1)F_1+(x_2+iy_2)F_2+(x_3+iy_3)F_3.$