Simple Construction of the Circle of Apollonius
Problem
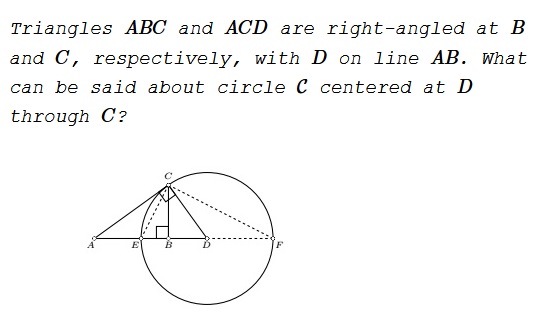
Solutions
$\mathcal{C}$ is the circle of Apollonius $\displaystyle \frac{XA}{XB}=\frac{CA}{CB}\,(\gt 1)$.
Indeed, with $\angle EDC=\angle BCA=2\varphi$ one has $\angle EFC=\angle BCE=\varphi$: $CE$ is the angle bisector of $\angle ACB$.
Another explanation is in that $A$ and $B$ are inverse images of each other about the circle of Apollonius $\mathcal{C}.$
Acknowledgment
The above construction, with a proof, has been devised by Grégoire Nicollier (UNIVERSITY OF APPLIED SCIENCES OF WESTERN SWITZERLAND).
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73582210
