Similar Triangles in Crossing Circles
What Might This Be About?
Problem
Circles $(O)$ and $(Q)$ cross at points $A$ and $B.$
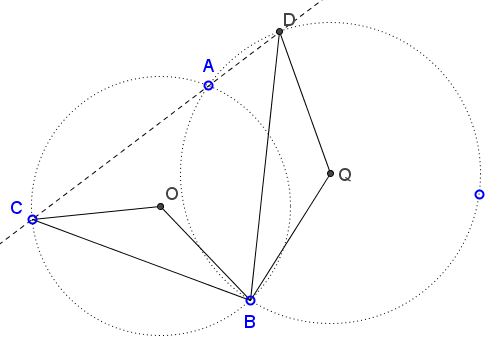
Prove that points $C$ on $(O)$ and $D$ on $(Q)$ are collinear with $A$ iff $\Delta COB \sim\Delta BQD.$
Solution
The problem is solved by simple angle chasing. Draw the common chord $AB.$

Inscribed $\angle BAC$ is half the central $\angle BOC.$
On the other hand, $\angle BAD$ is half the angular measure of the arc $BD$ that does not contain $A.$ In other words, it is supplementary to half the central $\angle BQD$ subtended by that arc $BD$ that does contain point $A.$ It follows that $\angle BQD=\angle BOC$ iff angles $BAC$ and $BAD$ are supplementary, i.e., iff $C,A,D$ are collinear.
Acknowledgment
This problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73615116
