Playing on Flanks
What Is This About?
And What Is This About?
Try Also This
Problem
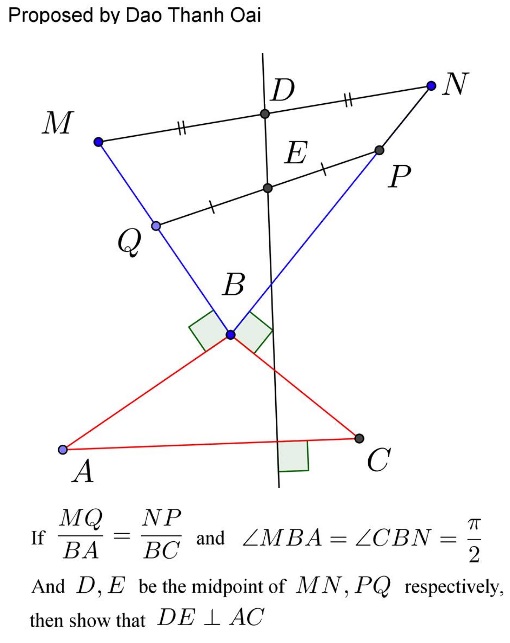
Solution 1
We have $\displaystyle \frac{A-B}{M-Q}=\frac{BA}{MQ}\cdot i=ki\,$ and $\displaystyle \frac{N-P}{C-B}=\frac{NP}{BC}\cdot i=\frac{i}{k}.\,$ It follows that $\displaystyle \frac{B-C}{N-P}=ki=\frac{A-B}{M-Q},\,$ hence,
$\displaystyle \frac{B-C}{N-P}=\frac{A-B}{M-Q}=\frac{(A-B)+(B-C)}{(M-Q)+(N-P)}=ki,$
such that $\displaystyle \frac{A-C}{2(D-E)}=ki\,$ and, finally, $DE\perp AC.$
Solution 2
Consider the following two coordinate systems:
- Unit vectors $\hat{x}$ and $\hat{y}$ along $BC$ and $BP$, respectively.
- Unit vectors $\hat{u}$ and $\hat{v}$ along $BQ$ and $BA$, respectively.
The orthogonal transformation between the two coordinate systems can be written for some angle $\phi$ as
$\displaystyle\begin{align}\hat{u}&=\hat{x}\cos\phi+\hat{y}\sin\phi \\ \hat{v}&=-\hat{x}\sin\phi+\hat{y}\cos\phi. \end{align}$
Thus,
$\displaystyle\begin{align} \hat{x}\cdot\hat{u}&=\cos\phi, \\ \hat{y}\cdot\hat{v}&=\cos\phi. \end{align}$
The different vectors can be written in these two systems as follows:
$\displaystyle\begin{align} \vec{BC}&=a\hat{x} \\ \vec{BP}&=p\hat{y} \\ \vec{BN}&=(p+ka)\hat{y} \\ \vec{BA}&=b\hat{v} \\ \vec{BQ}&=q\hat{u} \\ \vec{BM}&=(q+kb)\hat{u} \\ \vec{BE}&=\frac{1}{2}(p\hat{y}+q\hat{u}) \\ \vec{BD}&=\frac{1}{2}\left[(p\hat{y}+q\hat{u})+k(a\hat{y}+b\hat{u})\right] \\ \vec{ED}&=\vec{BD}-\vec{BE}=\frac{k}{2}(a\hat{y}+b\hat{u}) \\ \vec{AC}&=\vec{BC}-\vec{BA}=a\hat{x}-b\hat{v}. \end{align}$
$\displaystyle\begin{align} \vec{AC}\cdot\vec{ED} &=\frac{k}{2}(a\hat{x}-b\hat{v})\cdot(a\hat{y}+b\hat{u}) \\ &=\frac{k}{2}ab(\hat{x}\cdot\hat{u}-\hat{v}\cdot\hat{y}) \\ &=\frac{k}{2}ab(\cos\phi-\cos\phi)=0. \end{align}$
Solution 3
Step 1. There is a well studied property of flank triangles (triangles $MBN\,$ and $ABC\,$ below): the median through the common vertex in one is an altitude in another.
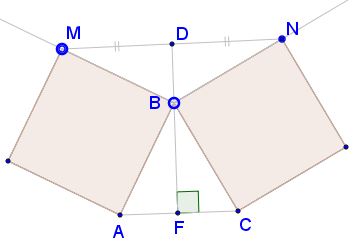
Step 2. If line $MN\,$ moves parallel to itself, line $DB\,$ remains fixed (due to Thales' theorem):
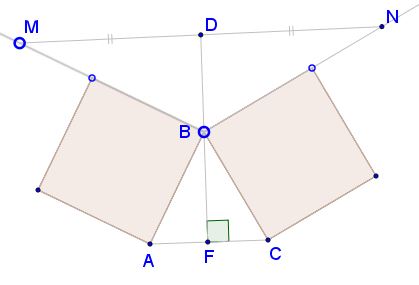
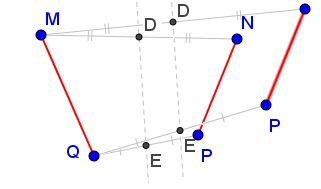
Step 3. Given two segments $MQ\,$ and $NP\,$ and the midpoints $D,E\,$ of $MN\,$ and $PQ,\,$ respectively. Then when the segments $MQ\,$ and $NP\,$ are moved, staying parallel to their initial positions, so does line $DE.\,$ When $P=Q,\,$ it's a property of flank triangles that $DB\perp AC.\,$ It follows that $DE\perp AC\,$ in a more general configuration.
Acknowledgment
The problem that is due to Dao Thanh Oai was posted at the CutTheKnotMath facebook page by Bo Cua Ga. This is an extension of the well studied properties of flank triangles. Solution 1 is by Leo Giugiuc.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73582003
