A Problem in Pentagon with Supplementary Angles

Much of the proof is based on angles chasing.

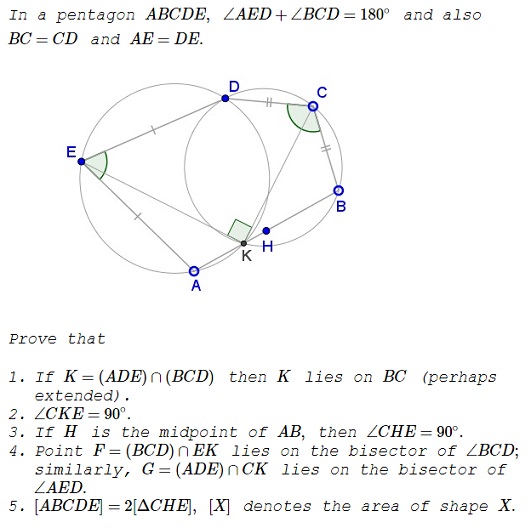
Join $D\,$ to $A,K,B.$

Since inscribed angles subtended by the same arc are equal,

$\displaystyle\begin{align} &\angle BKC=\angle BDC=\frac{1}{2}(180^{\circ}-\angle BCD),\\ &\angle CKD=\angle CBD=\frac{1}{2}(180^{\circ}-\angle BCD),\\ &\angle AKE=\angle ADE=\frac{1}{2}(180^{\circ}-\angle AED),\\ &\angle DKE=\angle DAE=\frac{1}{2}(180^{\circ}-\angle AED),\\ \end{align}$

Adding up we get

$\displaystyle\begin{align} \angle BKC+\angle CKD+\angle AKE+\angle DKE&=2\cdot 180^{\circ}-(\angle BCD+\angle AED)\\ &=2\cdot 180^{\circ}-180^{\circ}=180^{\circ}, \end{align}$

implying that $AKB\,$ is a straight line. This answers #1. Along the way, we obtain

$\displaystyle\angle BKC+\angle AKE=180^{\circ}-\frac{1}{2}(\angle BCD+\angle AED)=\frac{180^{\circ}}{2},$

implying $\angle CKE=90^{\circ},\,$ i.e. #2.

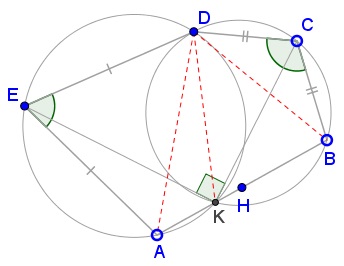
To prove #3, we mimic Solution 2 from an earlier page. Consider a sequence of rotations: around $E\,$ through $\angle AED,\,$ around $C\,$ through $\angle DCB,\,$ through $180^{\circ}\,$ around $H.\,$ The result is either a translation or a rotation which lives $A\,$ fixed. It follows that the composition of the three rotations is the identity transform.

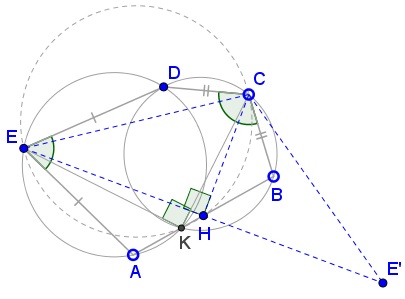
Let's trace $E:\,$ the first rotation leaves it stationary, the second moves it to some $E',\,$ the third takes $E'\,$ back to $E.\,$ It follows that $H\,$ is the midpoint of the base of the isosceles $\Delta ECE',\,$ such that $CH\perp EE',\,$ i.e., $\angle CHE=90^{\circ}.$

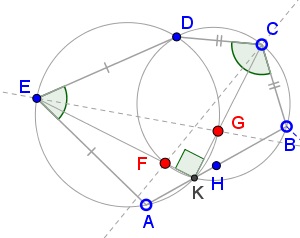
Lastly, $\angle CKF=\angle CKE=90^{\circ}.\,$ This makes $CF\,$ a diameter of $(BCD)\,$ and, since $B\,$ is the midpoint of one arc $\overset{\frown}{BD},\,$ $F\,$ is the midpoint of the other. Thus $CF\,$ is the bisector of $\angle BCD.$

Point $G\,$ is treated similarly. This proves #4. Join now $BE'.\,$ Since $H\,$ is the midpoint of both $EE'$ and $AB,\,$ $AEBE'\,$ is a parallelogram, so that $BE'=AE=DE.\,$

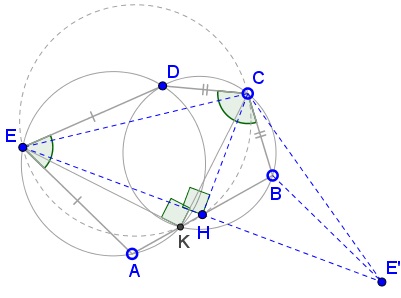
It follows that $\Delta BE'H=\Delta AEH\,$ and $\Delta BCE'=\Delta DCE.\,$ As we can see,

$\begin{align}[\Delta ECH] &= [\Delta E'CH]\\ &=[\Delta CBK]+[\Delta BE'H]+[\Delta BCE']\\ &=[\Delta CBK]+[\Delta AEH]+[\Delta DCE], \end{align}$

which implies #5.

The problem due Thanos Kalogerakis is a generalization of an earlier one. The problem was posted at the Peru Geometrico and, as #1082, Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook groups.