A Problem in Pentagon with Right Angles
What Is This About?
Source
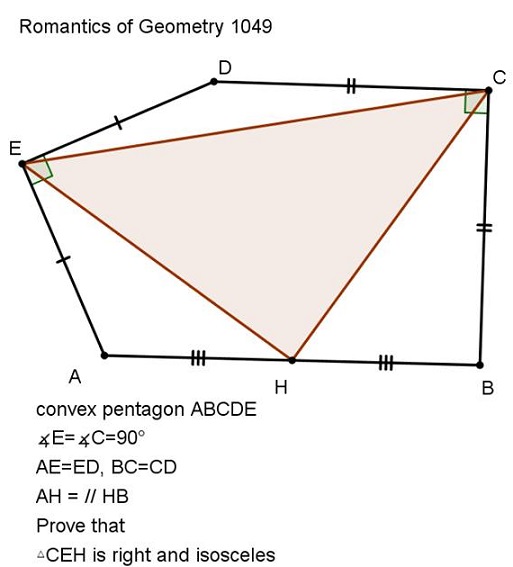
Problem
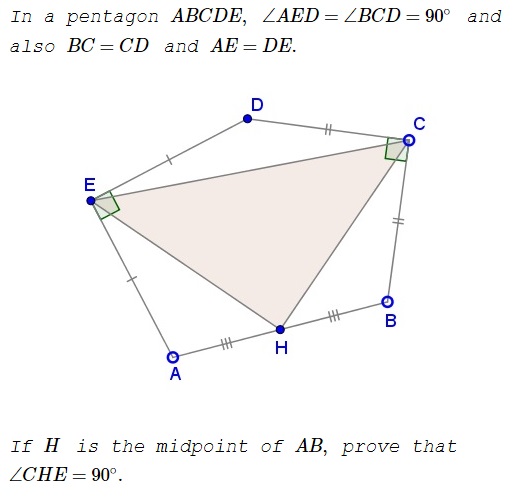
Solution 1
We'll use complex numbers, using lower case $x\,$ to represent point $X.\,$ From the condition on two angles and the geometric meaning of multiplication by $i,$
$d-c=i(b-c),\\ d-e=-i(a-e).$
Subtracting the second from the first and dividing by $2\,$ we get
$\displaystyle \frac{e-c}{2}=i\frac{a+b}{2}-i\frac{c+e}{2}$
which is the same as
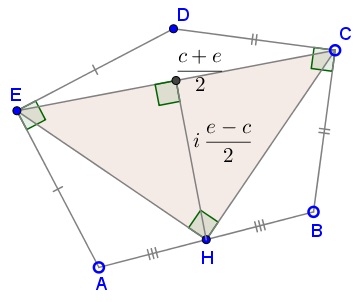
$\displaystyle h=\frac{c+e}{2}+i\frac{c-e}{2}.$
This exactly means that $\Delta CEH\,$ is right isosceles, $EH=CH\,$ and $\angle CHE=90^{\circ}.$
Solution 2
Consider a sequence of transformations: first rotate $90^{\circ}\,$ around $E\,$ (taking $A\,$ to $D),\,$ then rotate $90^{\circ}\,$ about $C\,$ (taking $D\,$ to $B),\,$ and finally rotate $180^{\circ}\,$ about $H\,$ taking $B\,$ to $A.\,$
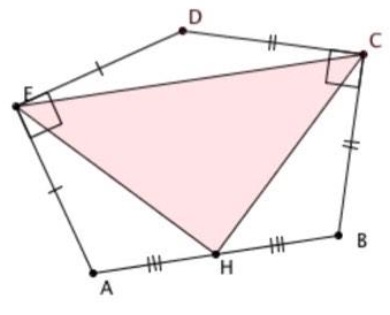
The resulting transformation, which is either the identity or a translation, must be the identity since it takes $A\,$ to $A.$
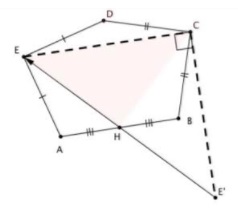
Now follow point $E:\,$ $E\,$ is fixed by the first rotation, then goes to $E',\,$ which then reflects across $H\,$ back to $E.$
Then $\Delta ECE'\,$ is an isosceles right triangle, and $CH\,$ is the median to the hypotenuse. Therefore, $CH\perp EH\,$ and $CH=EH.$
Add-on
Let $M\,$ be the midpoint of $AD,\,$ $N\,$ that of $BD.$
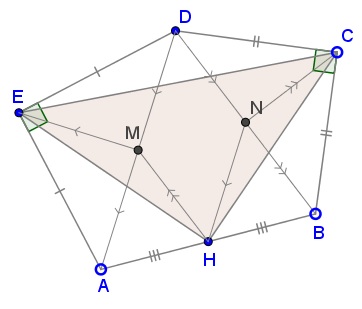
Then $\Delta HME=\Delta CNH.$
Acknowledgment
The problem was kindly posted at the CutTheKnotMath facebook page by Marian Dinca, with a suggestion to employ complex numbers for a short solution (Solution 1). Solution 2 is by Ted Courant. The problem appeared as Problem 1049 at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group.
Emil Stoyanov made an additional observation (Add-on) about equality of two triangles that emerged in the configuration at hand.
Remark
Thanos Kalogerakis came up with a generalization that sheds light on the essence of the problem:
In a pentagon $ABCDE,\,$ $\angle AED+\angle BCD=180^{\circ}\,$ and also $BC=CD\,$ and $AE=DE.$
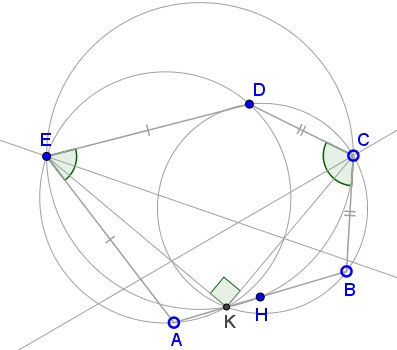
Prove that
- The point $K\,$ of intersection of the two circles $(ADE)\,$ and $(BCD)\,$ is on $AB;$
- Circle $(CEK)\,$ passes through the midpoint $H\,$ of $AB.$
We shall discuss this problem ">later on.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73561073
