A Property of Incenter Relative to Circumcircle
What Is This About?
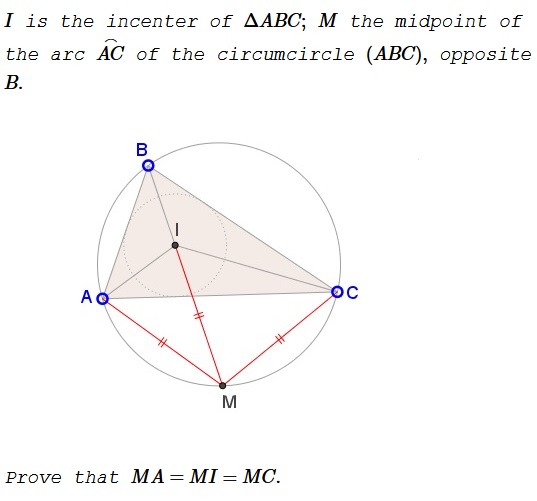
Problem
Solution
This is pure angle chasing. Let $N$ be the midpoint of the arc $\overset{\frown}{BC},$ so that $AN$ is the bisector of $\angle BAC$ and, thus, passes through $I.$
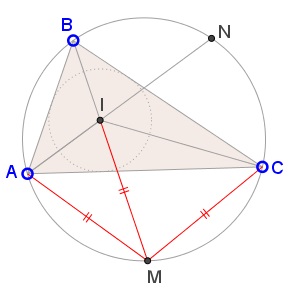
Let angles at $A,$ $B,$ $C$ be $2\alpha,$ $2\beta,$ $2\gamma,$ respectively. $\alpha+\beta+\gamma=90^{\circ}.$ Then
- $\angle IAM=\angle NAM=\angle NAC+\angle MAC=\angle NAC+\angle MBC=\alpha+\beta.$
- $\angle AMI=\angle AMB=\angle ACB=2\gamma.$
From these two,
$\begin{align}\angle AIM&=180^{\circ}-\angle IAM-\angle AMI\\ &=180^{\circ}-(\alpha+\beta)-2\gamma=\alpha+\beta\\ &=\angle IAM. \end{align}$
It follows that $\Delta ABC$ is isosceles and $MA=MI.$ Since $M$ is the midpoint of $\overset{\frown}{AC},$ $MA=MC$ and this completes the proof.
Acknowledgment
This is a well-known fact that I recently came across in a proof by Luis Alberto Sagua Cruz of a by far more complicated problem at the Peru Geometrico facebook group. Under a slightly different guise the problem was treated elsewhere at the site.
I am grateful to Konstantin Knop for providing extra references. It so happens that the above fact is a part of a more general statement.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73512234
