Tangent to the Incircle
Problem
Let $ABC$ be an isosceles triangle, with the base angle $\alpha$ and incircle $\Gamma$. $D$ and $E$ are points on the sides $AB$ and $AC$ such that $DE$ is tangent to $\Gamma.$
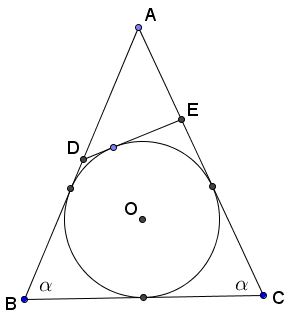
Show that $\displaystyle\frac{AD}{DB}+\frac{AE}{EC}=\frac{1-\cos\alpha}{\cos\alpha}$
Lemma
$PA,PB,PC$ are three chords in a circle, $\angle APB=\angle APC=\phi.$
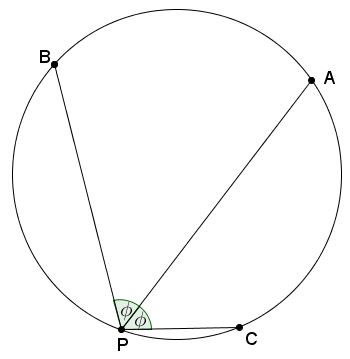
Then $\displaystyle\frac{PB+PC}{PA}=2\cos\phi.$
Proof of Lemma
Let $O$ be the center of the circle, $AD$ a diameter. Introduce $\beta=\angle DCP=\angle DAP.$ In right $\Delta ADP,$ $AP=AD\cdot\cos\beta=2R\cos\beta,$ where R is the radius of circle $(O).$
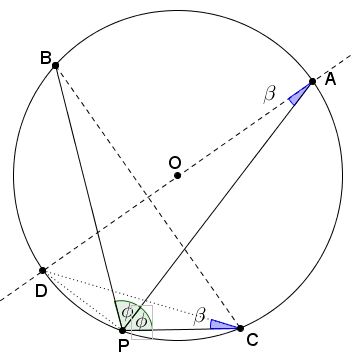
In $\Delta BCP,$ $\angle BCP=90^{\circ}-\phi +\beta,$ $\angle CBP=90^{\circ}-\phi -\beta,$ (or the other way round). By the Law of Sines,
$\displaystyle\frac{PB}{\sin(90^{\circ}-\phi +\beta)}=\frac{PC}{\sin(90^{\circ}-\phi -\beta)}=2R.$
Since $\sin(90^{\circ}-\phi \pm\beta)=\cos\phi\cdot\cos\beta\mp\sin\phi\cdot\sin\beta,$ we have
$PB+PC=4R\cdot\cos\phi\cdot\cos\beta,$
Dividing by $AP=2R\cos\beta$ proves the lemma.
Proof 1
Joint $O$ to $D$ and $E$ and let $K,L,M$ be the points of tangency of $(O),$ as shown.
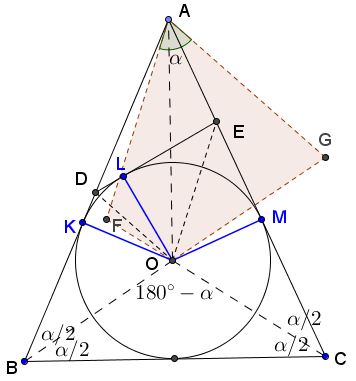
$\angle KAM=180^{\circ}-2\alpha$ so that $\angle KOM=2\alpha.$ Further, $OD$ bisects $\angle KOL,$ $OE$ bisects $\angle LOM,$ implying that $\angle DOE=\alpha .$
Draw $AF\parallel OE$ and $AG\parallel OD,$ where $F$ is on $CO,$ $G$ on $BO,$ both produced. First of all, note that, by the construction, $\angle FAG=\angle DOE=\alpha.$ Second of all, $\angle FOG=\angle BOC=180^{\circ}-\alpha.$ It follows that $\angle FAG+\angle FOG=180^{\circ},$ making quadrilateral $AFOG$ cyclic. Finally note that $OA$ bisects $\angle FOG$ because $O$ is the incenter of $\Delta ABC.$
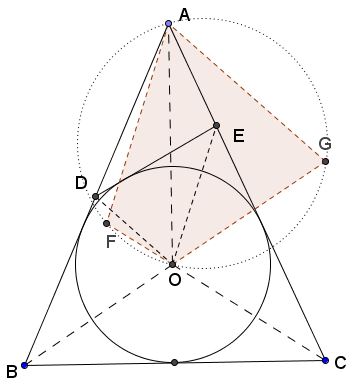
We are in a position to apply Lemma to $AFOG$ in $(AFOG),$ with $\phi=\angle AOF=90^{\circ}-\alpha /2:$
$\displaystyle\frac{OF+OG}{OA}=2\cos(90^{\circ}-\frac{\alpha}{2})=2\sin\frac{\alpha}{2}.$
On the other hand, since $AF\parallel OE$ and $AG\parallel OD,$ $\displaystyle\frac{AD}{DB}=\frac{GO}{OB}$ and $\displaystyle\frac{AE}{EC}=\frac{FO}{OC},$ by Thales' theorem. Taking into account that $OB=OC$ and using the Law of Sines in $\Delta AOB,$ the we obtain
$\begin{align}\displaystyle \frac{AD}{DB}+\frac{AE}{EC}&=\frac{GO+FO}{OB}\\ &=\frac{OA\cdot 2\sin\frac{\alpha}{2}}{OB}\\ &=2\sin\frac{\alpha}{2}\cdot\frac{\sin\angle ABO}{\sin\angle BAO}\\ &=2\sin\frac{\alpha}{2}\cdot\frac{\sin\frac{\alpha}{2}}{\sin(90^{\circ}-\alpha)}\\ &=\frac{1-\cos\alpha }{\cos\alpha}, \end{align}$
as required.
Proof 2
Notice that
$\displaystyle\frac{DA}{DB}+\frac{EA}{EC}=\frac{AB}{DB}+\frac{AC}{EC}-2.$
Set $AB\cap\Gamma=\{K\}$, $DE\cap\Gamma=\{L\}$, $\angle KOL=\epsilon$, and $BC=2$.
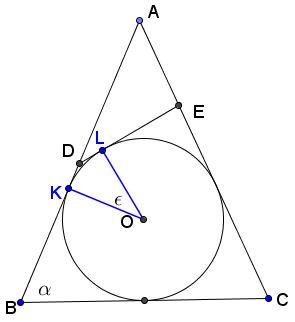
Using
$AB=AC=\sec\alpha,\\ DB=1+\tan\frac\alpha2\tan\frac\epsilon2,\\ EC=1+\tan\frac\alpha2\tan\left(\alpha-\frac\epsilon2\right),\\ 1+\tan\gamma\tan\delta=\sec\gamma\sec\delta\cos(\gamma-\delta),\\ \cos\frac\epsilon2+\cos\left(\alpha-\frac\epsilon2\right)=2\cos\frac\alpha2\cos\left(\frac{\alpha-\epsilon}2\right),\,\mbox{and}\\ 2\cos^2\frac\alpha2=1+\cos\alpha ,$
one gets at once that
$\begin{align}\displaystyle \frac{AB}{DB}&+\frac{AC}{EC}-2\\ &= \frac{\sec\alpha}{1+\tan\frac{\alpha}{2}\tan\frac{\epsilon}{2}}+ \frac{\sec\alpha}{1+\tan\frac{\alpha}{2}\tan(\alpha-\frac{\epsilon}{2})}-2\\ &=\frac{\sec\alpha}{\sec\frac{\alpha}{2}\sec\frac{\epsilon}{2}\cos(\frac{\alpha}{2}-\frac{\epsilon}{2})}+\frac{\sec\alpha}{\sec\frac{\alpha}{2}\sec(\alpha-\frac{\epsilon}{2})\cos(\frac{\alpha}{2}-\frac{\epsilon}{2})}-2\\ &=\frac{\sec\alpha\cos\frac{\alpha}{2}}{\cos(\frac{\alpha}{2}-\frac{\epsilon}{2})}\bigg(\cos\frac{\epsilon}{2}+\cos(\alpha-\frac{\epsilon}{2})\bigg)-2\\ &=\frac{\sec\alpha\cos\frac{\alpha}{2}}{\cos(\frac{\alpha}{2}-\frac{\epsilon}{2})}\cdot2\cos\frac{\alpha}{2}\cos(\frac{\alpha}{2}-\frac{\epsilon}{2})-2\\ &=2\sec\alpha\,\cos^{2}\frac{\alpha}{2}-2\\ &=\sec\alpha (1+\cos\alpha)-2\\ &=\sec\alpha-1\\ &=\frac{KA}{KB}. \end{align}$
Proof 3
Let $\{X\}=BE\cap CD,$ $\{Y\}=AX\cap BC.$
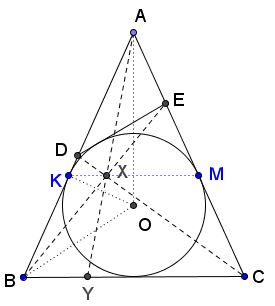
From a theorem credited to Newton, $X\in KL.$ Thus, from van Aubel's theorem,
$\displaystyle\frac{AD}{DB}+\frac{AE}{EC}=\frac{AX}{XY}=\frac{AK}{KB}.$
Further,
$\displaystyle \frac{AK}{KB}=\frac{\tan\alpha}{\cot\frac{\alpha}{2}}=\tan\alpha\cdot\sqrt{\frac{1-\cos\alpha}{1+\cos\alpha}}=\frac{1-\cos\alpha}{\cos\alpha}.$
Proof 4
Denote $DE=a,$ $AD=c,$ and $AE=b.$
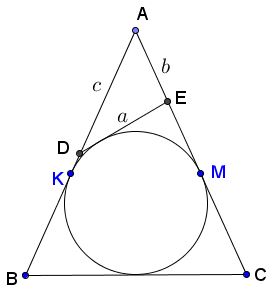
Then $(O)$ is an excircle of $\Delta ADE.$ Set $AD\cap (O)={K}$ and $AE\cap (O)={M}.$ If $p$ is the semiperimeter of $\Delta ADE,$ then $AK=AM=p$ whereas $\sin\frac{A}{2}=\cos\alpha ,$ implying $KM=2p\,\cos\alpha .$
Since triangles $ABC$ and $AKM$ are similar, $\displaystyle\frac{p}{p+KB}=\frac{2p\cos\alpha}{2KB},$ implying $\displaystyle KB=\frac{p\cos\alpha}{1-\cos\alpha}.$ In other words,
$\displaystyle DB=p-c+\frac{p\cos\alpha}{1-\cos\alpha}=\frac{p-c+c\cos\alpha}{1-\cos\alpha}.$
Similarly, $\displaystyle EC=\frac{p-b+b\cos\alpha}{1-\cos\alpha}.$ So we have to prove that
(*)
$\displaystyle \frac{c}{p-c+c\cos\alpha}+\frac{b}{p-b+b\cos\alpha}=\frac{1}{\cos\alpha}.$
With $\displaystyle\cos\alpha=\sin\frac{A}{2}=\sqrt{\frac{(p-b)(p-c)}{bc}},$ this is immediate.
Proof 5
Denote $X\in BE\cap CD$ and $Y\in AX\cap BC.$ Apply Newton's theorem to $BDEC,$ i.e. $X\in KM.$ Now I'll use van Aubel's theorem with $X$ in $\triangle ABC:$
$\displaystyle\frac {DA}{DC}+\frac {EA}{EC}= \frac {XA}{XY}$
because $KM\parallel BC.$
$\displaystyle\frac {XA}{XY}=\frac {TA}{TB},$ i.e, $\displaystyle\frac {DA}{DC}+\frac {EA}{EC}=\frac {KA}{KB}.$ Thus,
$\displaystyle\frac {KA}{KB}+1=\frac {AB}{KB}= \frac {AB}{BM}=\frac 1{\cos B}.$
So that
$\displaystyle\frac {KA}{KB}=\frac 1{\cos B}-1= \frac {1-\cos B}{\cos B},$
or,
$\displaystyle\frac {KA}{KB}=\frac {1-\cos B}{\cos B}$
and, finally,
$\displaystyle\frac {DA}{DB}+ \frac {EA}{EC}=\frac {1-\cos B}{\cos B}.$
Generalization
Let $\triangle ABC$ with the incircle $(O)$ and two points $D\in AB,$ $E\in AC$ such that $DE$ is tangent to $(O).$ Then
$\displaystyle (p-b)\cdot \frac {DA}{DB}+(p-c)\cdot\frac {EA}{EC}=(p-a),$
where $p$ is the semiperimeter of $\Delta ABC$ whose sides are, as usual, $a,b,c.$
Acknowledgment
The problem have been proposed by Miguel Ochoa Sanchez (Peru) who posted it along with Proof #1 at the CutTheKnotMath facebook page. This is a generalization of Problem 1 from the second day of the IberoAmerican 1993 olympiad. The original problem dealt with an equilateral triangle.
Proof #2 was kindly communicated to me by Grégoire Nicollier. Proof #3 is by Telv Cohl, proof #4 is by Leo Giugiuc. Both have been posted to the artofproblemsolving site.
Proof 5 and the generalization are due to Virgil Nicula who gave two proofs of the latter.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578925
