Homothety in Three Tangent Circles II
What Is This About?
11 March 2017, Created with GeoGebra
Problem
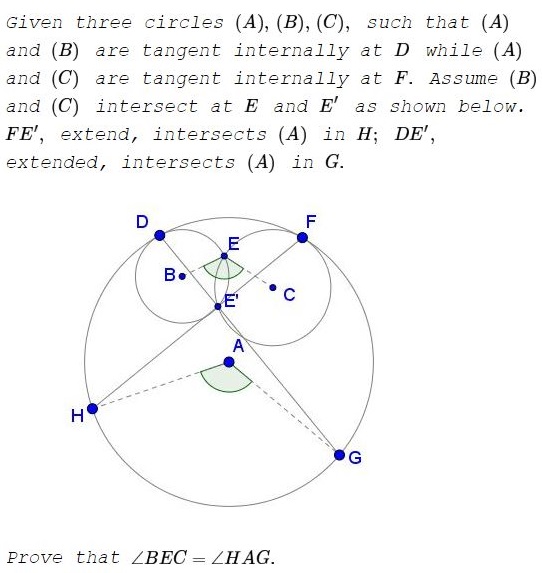
Solution
Join $D\,$ to $H\,$ and $F\,$ to $G.\,$ Let $I\,$ be the second intersection of $DH\,$ with $(B);\,$ let $J\,$ be the second intersection of $FG\,$ with $(C).\,$
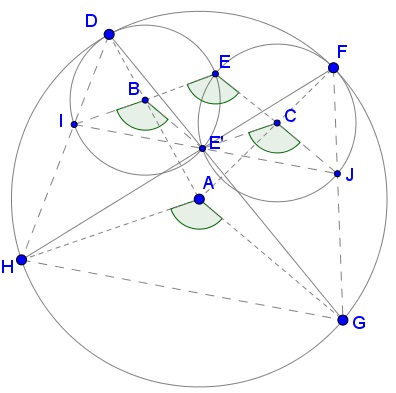
Circle $(A)\,$ is obtained from $(B)\,$ by a homothety with center $D\,$ such that $IE'\parallel HG.\,$ Similarly, also $E'J\parallel HG.\,$ In addition, angles $HDG\,$ and $HFG\,$ are subtended by the same arc in $(A),\,$ implying $\angle IDE'=\angle E'FJ.$
It follows that the corresponding central angles are also equal: $\angle ABE'=\angle E'CJ.\,$ Triangles $ABE'\,$ and $E'CJ\,$ are isosceles and have equal apex angles, such that their base angles are also equal: $\angle BE'I=\angle JE'C.\,$ It follows that
$\displaystyle \begin{align} \angle BEC &= \angle BE'C = 180^{\circ}-\angle BE'I-\angle JE'C\\ &=180^{\circ}-\frac{1}{2}(180^{\circ}-\angle IBE')-\frac{1}{2}(180^{\circ}-\angle E'CJ)\\ &= \frac{1}{2}(\angle IBE'+\angle E'CJ),\,\text{but the two angles are equal to}\,\angle HAG\\ &=\angle HAG. \end{align}$
Acknowledgment
This problem is a generalization of another one which I learnt about from a tweet by Tim Brzezinski, with a dynamic illustration of the problem posted by Antonio Gutierrez.
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73582353
