Homothety in Three Tangent Circles

What Is This About?

11 March 2017, Created with GeoGebra

Problem

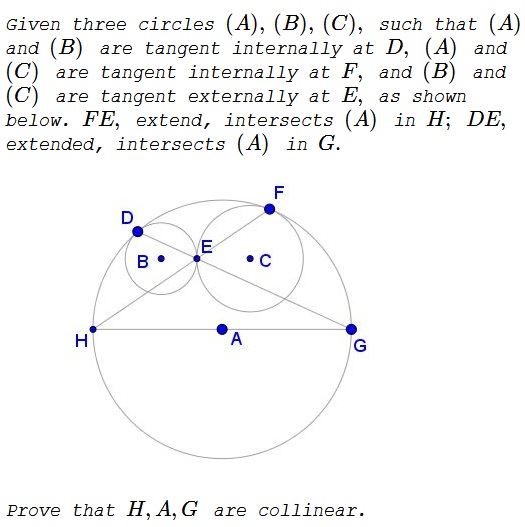
Homothety in Three Tangent Circles, problem

Solution 1

Join $D\,$ and $F\,$ to $A.\,$ Due to the tangency of the circles, $B\in AD\,$ and $C\in AF.$

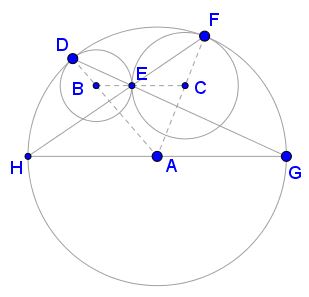
Homothety in Three Tangent Circles, solution 1

Circle $(A)\,$ is obtained from $(B)\,$ by a homothety with center $D\,$ such that $BE\parallel AG.\,$ Similarly $EC\parallel HA.\,$ However, since circles $(B)\,$ and $(C)\,$ are tangent at $E,\,$ $E\in BC.\,$ In other words, $B,\,$ $E\,$ $C\,$ are collinear, implying that so are $H,\,$ $A,\,$ and $G.$

Solution 2

The problem is a particular case of a more general one, treated on a separate page:

Given three circles $(A),\,(B),\,(C),\,$ such that $(A)\,$ and $(B)\,$ are tangent internally at $D\,$ while $(A)\,$ and $(C)\,$ are tangent internally at $F.\,$ Assume $(B)\,$ and $(C)\,$ intersect at $E\,$ and $E'\,$ as shown below. $FE',\,$ extend, intersects $(A)\,$ in $H;\,$ $DE',\,$ extended, intersects $(A)\,$ in $G.$

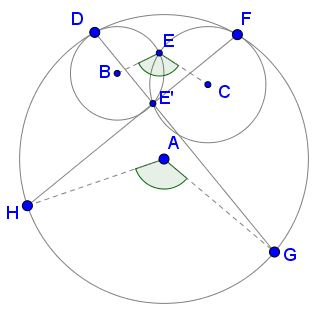
Homothety in Three Tangent Circles, 2

Prove that $\angle BEC=\angle HAG.$

Obviously, $(B)\,$ and $(C)\,$ are tangent at $E,\,$ if and only if $\angle BEC=180^{\circ},\,$ which reduces to the previous problem.

Acknowledgment

I learned of this problem from a tweet by Tim Brzezinski, with a dynamic illustration of the problem posted by Antonio Gutierrez.

72185009