Heron in Trapezoid
What Is It About?
Problem
The applet purports to illustrate the following statement:
$APB\;$ is an isosceles triangle with $AP=BP;\;$ $\ell\;$ is a line through $P,\;$ not meeting $\Delta APB\;$ otherwise. At point $M\;$ on $AB\;$ draw two rays that intersect $\ell\;$ in $C\;$ and $D,\;$ respectively, such that $\angle BMC=\angle AMD=90^{\circ}-\frac{1}{2}\angle APB.\;$
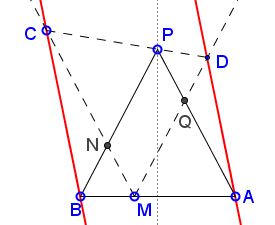
Then $AD\parallel BC.$
Proof 1
As an aside, $M\;$ solves Heron's problem for $C,\,D\;$ and the line $AB.\;$ It is, therefore, uniquely defined for given $C\;$ and $D,\;$ regardless whether or not angles $BMC\;$ and $AMD\;$ have been specified beyond being equal.

We have $CM\parallel AP\;$ and $DM\parallel BP\;$ so that triangles $CNP\;$ and $PQD\;$ are similar. In addition, $BN=MN=PQ\;$ and $AQ=MQ=NP.\;$ THe quadrilateral $MNPQ\;$ is a parallelogram.
Further, $\displaystyle\frac{CN}{PQ}=\frac{NP}{DQ},\;$ or, $\displaystyle\frac{CN}{BN}=\frac{AQ}{DQ}.\;$ Also, $\angle BNC=\angle MNP=\angle MQP=\angle AQD.\;$ It follows that the triangles $BNC\;$ and $DQA\;$ are similar. Two pairs of their sides are parallel, and, therefore, so is the third pair: $BC\parallel AD.$
Proof 2
In the hexagon $BPADMC\;$ whose vertices alternate on two lines $AB\;$ nd $CD,\;$ two pairs of sides are parallel by the construction, meaning their intersections lie on the line at infinity. By Pappus' theorem so does the intersection of the third pair of sides.
Remark
The problem just discussed is the basis for a proof (Proof 2) of an engaging problem invented by Miguel Ochoa Sanchez.
Acknowledgment
Proof 2 is by Grégoire Nicollier.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73614991
