Multiplication of Points on a Circle
What is this about?
Problem
In a cyclic hexagon $IDMNPB,$ $IB\parallel MN$ and $ID\parallel NP.$
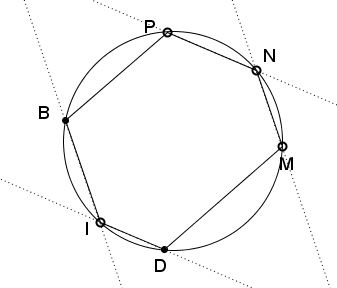
Prove that $BP\parallel DM.$
Proof
$\angle BID=\angle MNP,$ since their sides are parallel. The two angles then are subtended by equal chords: $BD=MN.$
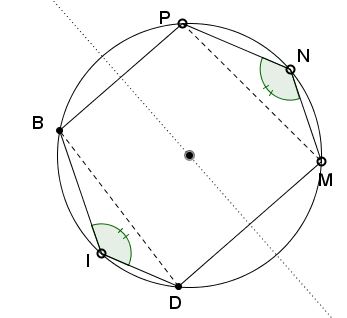
If $P$ is the point of intersection of $BD$ and $MN$ (which might be at infinity) and $O$ is the center of the circumscribed circle, then $BD$ and $MN$ are symmetric reflections of each other in $OP.$ This implies that $OP\perp BP$ and also $OP\perp DM,$ implying that $BP\parallel DM.$
An application
Given circle $(O)$ and point $I\in (O).$ For any two points $M$ and $N$ on $(O)$ define a third point $M*N$ such that the chord from $I$ to $M*N$ is parallel to $MN.$
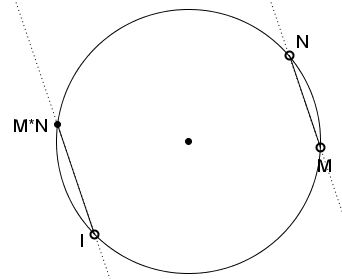
Prove that "*" is a binary operation that defines an abelian group on $(O).$
Indeed, commutativity of "*" is obvious. $I$ plays the role of unity. The inverse of a point is the point symmetric to it in the diameter through $I.$ (This is of course if a tangent to a circle is thought of as passing twice through the point of tangency.)
The statement above helps prove the associativity of "*".
Let there be three points $M,$ $N,$ $P.$ By the definition, the chords from $I$ to $M*N$ and $N*P$ are parallel to $MN$ and $NP,$ respectively.
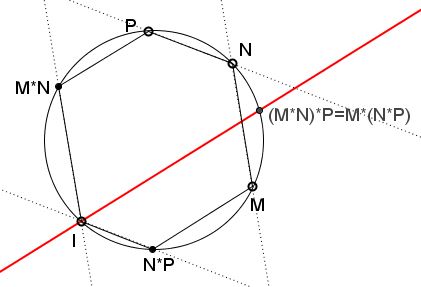
In the cyclic hexagon formed by six points $I,$ $N*P,$ $M,$ $N,$ $P,$ $M*N$ two pairs of opposite sides are parallel. By the statement proved above this implies that the third pair of opposite sides are also parallel. Thus the chords from $I$ parallel to $M*N,P$ and $M,N*P$ coincide, meaning that $(M*N)*P=M*(N*P).$
Generalization
Telv Cohl has commented on the above statement that it is a particular case of Pascal's theorem, which stipulates that the intersections of the opposite sides of a hexagon inscribed in a conic are collinear. This, in particular, implies that, if two of the intersections lie at infinity, then so is the third. As a consequence, the statement holds for an ellipse, or any other conic.
Acknowledgment
The problem stemmed from the one posted at the CutTheKnotMath facebook page by Leo Giugiuc (Romania). Leo, posted the problem for an ellipse and supplied an elegant algebraic solution.
What Can Be Multiplied?
- What Is Multiplication?
- Multiplication of Equations
- Multiplication of Functions
- Multiplication of Matrices
- Multiplication of Numbers
- Peg Solitaire and Group Theory
- Multiplication of Permutations
- Multiplication of Sets
- Multiplication of Vectors
- Multiplication of a Vector by a Matrix
- Vector Space and Spaces with the Scalar Product
- Addition and Multiplication Tables in Various Bases
- Multiplication of Points on a Circle
- Multiplication of Points on an Ellipse
|Contact| |Front page| |Contents| |Geometry| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73574617
