Cevians and Conic through Six Points on Sidelines of Triangle
What is this about?
7 July 2013, Created with GeoGebra
Problem
In $\Delta ABC$ cevians $AD$, $BE$, and $CF$ meet at point $W$.
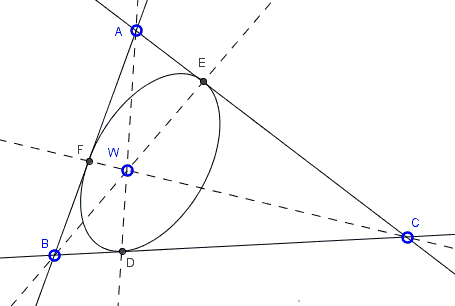
Prove that there is a conic tangent to $BC$ at $D,$ $AC$ at $E,$ and $AB$ at $F.$
Hint
If the statement is correct, and there is indeed a conic through the six points, you can change the configuration to a more convenient one by an affine transformation without disturbing its essential properties: the cevians remain concurrent, the points on each side remain equidistant from the feet of the cevians, the ellipse passes through six points.
Solution
To start off, I'll use the same approach that worked so well in case where points $D,E,F$ were the midpoints of the sides of $\Delta ABC.$ Make an affine transformation that maps $\Delta ABC$ on to the right isosceles triangles with vertices $(0,0),$ $(1,0),$ $(0,1),$ with points $D,F,E$ at $(m,0),$ $(0,n),$ and $(u,v),$ respecively; $u+v=1.$

By Ceva's theorem, $\frac{1-n}{n}\cdot\frac{m}{1-m}\cdot\frac{v}{1-v}=1,$ or, which is the same, $\frac{1-n}{n}\cdot\frac{m}{1-m}\cdot\frac{1-u}{u}=1.$ Thus, we can express $u$ and $v$ in terms of $m$ and $n:$
$u=\frac{mn}{(1-m)(1-n)+mn}$, $v=\frac{(1-m)(1-n)}{(1-m)(1-n)+mn}.$
As before, we are going to look for a conic (if such exists) through the six points. A conic is given by a second degree equation:
$ax^{2}+2bxy+cy^{2}+2dx+2ey+f=0,$
with only $5$ coefficients independent (because the conic would not change after the equation was divided by one of non-zero coefficients.)
Let's substitute the coordinates of points $G,H,I,J,K,L$ into the equation:
$a(m\pm h)^{2}+2d(m\pm h)+f=0,$
$c(n\pm i)^{2}+2e(n\pm i)+f=0,$
$a(u\pm j)^{2}+2b(u\pm j)(v\mp j)+c(v\mp j)^{2}+2d(u\pm j)+2e(v\mp j)+f=0.$
Unfold the first equation into two:
$a(m^{2}+2mh+h^{2})+2d(m+h)+f=0,$ and
$a(m^{2}-2mh+h^{2})+2d(m-h)+f=0.$
Solving these for $a$ and $d$ gives
$a = f/(h^{2}-m^{2}), $
$d = -ma.$
Similarly, unfolding the second pair of equations, we obtain
$c = f/(i^{2}-n^{2}), $
$e = -nc.$
Adding and subtracting the two unfolded equations for $I$ and $J$ gives
$a(u^{2}+j^{2})+2b(uv-j^{2})+c(v^{2}+j^{2})+2ud+2ve+f=0,$ and
$aj-cj+dj-ej=0,$
the latter of which holds automatically because, as we found, $a+d=c+e=0.$ From the former we can find the remaining coefficient $b$ in terms of $f.$ The six points $G,H,I,J,K,L$ determine a unique ellipse.
Acknowledgment
This problem generalizes the previously considered case where points $D,E,F$ were the midpoints of the sides of $\Delta ABC.$ The current problem, as the previous one, has been suggested by Dao Thanh Oai at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73586594
