Beyond Pythagoras

What is this about?

Problem

Let $ABC$ be a triangle with circumcenter $O;$ $X$ the intersection of the internal angle bisector of $\angle BAC$ and the perpendicular bisector of $BC.$ $Y$ and $Z$ lie on the external angle bisector of $\angle BAC$ such that $OY\parallel AB$ and $OZ\parallel AC.$

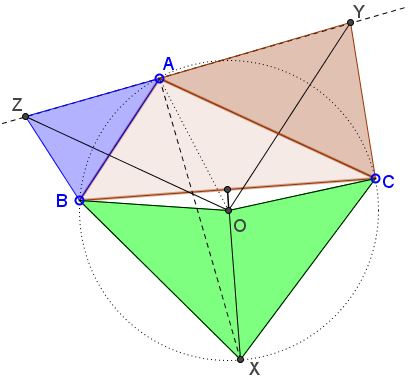
a generalization of the Pythagorean theorem by Tran Quang Hung, problem

Prove that $[ABZ]+[CAY]=[OBXC]$ where $[W]$ denotes the area of figure $W.$

Pythagorean theorem

Note that in case $\angle BAC = 90^{\circ}$ the above statement reduces to the Pythagorean theorem.

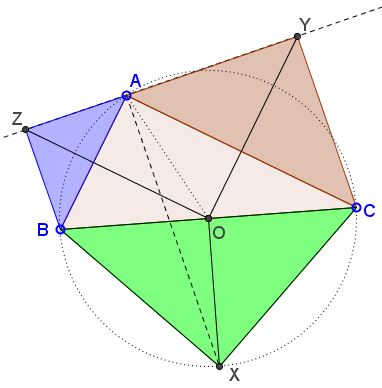
a generalization of the Pythagorean theorem by Tran Quang Hung, indeed a generalization

In this case $O$ lies on the hypotenuse $BC$ such that the quadrilateral $BOCX$ degenerates into triangle $BCX;$ and each of the triangles $ABZ,$ $CAY,$ $BCX$ is just a quarter of the square on the corresponding side.

Solution

By the construction, $AO=BO=CO=OX,$ giving four isosceles triangles $BOX,COX,AOC, AOB.$ For convenience let $\angle BAC=\alpha,$ $\angle AOY=\tau,$ $\angle AOZ=\rho.$

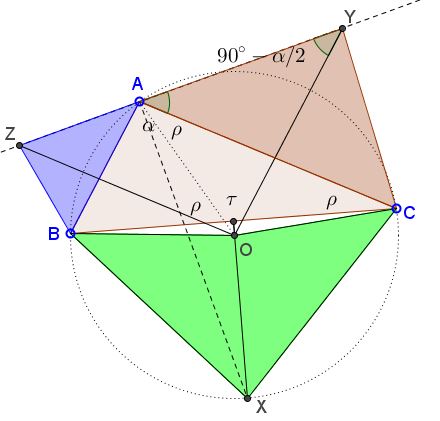
a generalization of the Pythagorean theorem by Tran Quang Hung, indeed a solution

Then, since OZ\parallel AC,$ $\angle CAO=\angle ACO=\rho.$ Also, since $YZ$ is the external bisector of $\angle BAC,$ $\angle BAZ=\angle CAY=90^{\circ}-\frac{1}{2}\alpha,$ implying that $\angle AYO=90^{\circ}-\frac{1}{2}\alpha$ also.

Now, by the Law of Sines, in $\Delta AOY,$

$\displaystyle\frac{AO}{\sin (90^{\circ}-\frac{1}{2}\alpha )}=\frac{AY}{\sin\tau},$ i.e., $\displaystyle\frac{AO}{\cos\frac{1}{2}\alpha}=\frac{AY}{\sin\tau}.$

In $\Delta AOC,$

$AC=2AO\cos\rho.$

Finally, $[ACY]=\frac{1}{2}AY\cdot AC\sin (90^{\circ}-\frac{1}{2}\alpha )=\frac{1}{2}AY\cdot AC\cos \frac{1}{2}\alpha.$ Combining the three formulas we obtain

$[ACY]=AO^{2}\sin\tau\cos\rho.$

Similarly, $[ABZ]=AO^{2}\sin\rho\cos\tau.$ Now, taking into account that $\tau +\rho =\alpha$ and applying the addition formula for sine,

$[ACY]+[ABZ]=AO^{2}(\sin\tau\cos\rho +\sin\rho\cos\tau )=AO^{2}\sin\alpha.$

To complete the proof, observe that figure $OBXC$ combines two isosceles triangles $BOX$ and $COX;$ the area of each is $\frac{1}{2}AO^{2}\sin\alpha,$ because both central angles $BOX$ and $COX$ equal $\alpha.$

Acknowledgment

The problem has been posted by Tran Quang Hung at the CutTheKnotMath facebook page.

71945713