Asymmetric Propeller of Squares
What Is This About?
Source
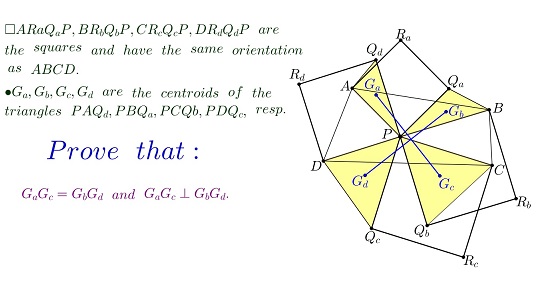
Problem
Given four similarly oriented squares that share a vertex: $APQ_aR_a,$ $BPQ_bR_b,$ $CPQ_cR_c,$ $DPQ_dR_d,$ consider the centroids $G_a,$ $G_b,$ $G_c,$ $G_d$ of triangles $APQ_d,$ $BPQ_a,$ $CPQ_b,$ $DPQ_c,$ respectively.
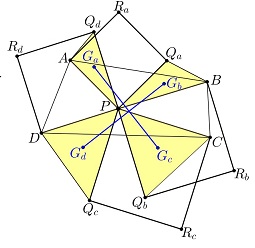
Prove that
$G_aG_c=G_bG_d$ and $G_aG_c\perp G_bG_d.$
Solution 1
Set in complex numbers $A=a,$ $B=b,$ $C=c,$ $D=d,$ and $P=0.$ Then $Q_a=-ai,$ $Q_b=-bi,$ $Q_c=-ci,$ $Q_d=-di.$ It follows that $3G_a=a-di,$ $3G_b=b-ai,$ $3G_c=c-bi,$ $3G_d=d-ci.$ Thus we have
$\begin{align} 3(G_a-G_c)&= (a-c)+(b-d)i,\\ 3(G_b-G_d)&=(b-d)+(c-a)i, \end{align}$
implying $G_a-G_c=(G_b-G_d)i,$ which proves the required statement.
Solution 2
We apply a theorem of squares on the sides of a quadrilateral in case where the quadrilateral degenerated into a point, specifically point $P.$ Let $H_a,$ $H_b,$ $H_c,$ $H_d$ be the midpoints of $AQ_d,$ $BQ_a,$ $CQ_b,$ and $DQ_c,$ respectively. Then $H_aH_c=H_bH_d$ and $H_aH_c\perp H_bH_d.$
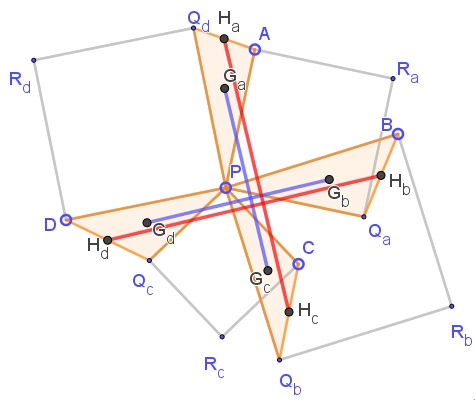
Further, $\displaystyle G_a=\frac{1}{3}(P+2H_a),$ $\displaystyle G_b=\frac{1}{3}(P+2H_b),$ $\displaystyle G_c=\frac{1}{3}(P+2H_c),$ $\displaystyle G_d=\frac{1}{3}(P+2H_d).$ We have,
$\displaystyle \begin{align} G_a-G_c&=\frac{2}{3}(H_a-H_c),\\ G_b-G_d&=\frac{2}{3}(H_b-H_d). \end{align}$
In other words, $\displaystyle G_aG_c=\frac{2}{3}H_aH_c=\frac{2}{3}H_bH_d=G_bG_d$ and, since $H_aH_c\perp H_bH_d,$ we also have $G_aG_c\perp G_bG_d.$
Acknowledgment
This problem by SPt Ân (Vietnam) was kindly communicated to me by Leo Giugiuc (Romania), along with a solution of his (Solution 1). The problem was originally posted at the Peru Geometrico facebook group. Additional solutions may be found at the link.
Alexandr Skutin found an error in Solution 2 and suggested a generalization of the problem.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73564110
