Angles in 4-5-6 Triangle
Problem
If the sides of a triangle are $4,5,6$ prove that the largest angle is exactly double the smallest angle.
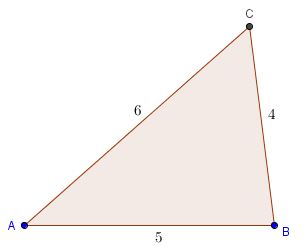
Solution 1
Let the largest angle (denoted $\beta$) be at vertex $B$, the smallest (denoted $\alpha$) at $A.$ Draw the altitude $CD.$
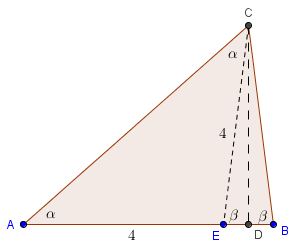
Set $CD=h$ and $BD=x.$ By the Pythagorean Theorem in triangles $ACD$ and $BCD,$
$\begin{align} h^{2}&=6^{2}-(5-x)^{2} \\ h^{2}&=4^{2}-x^{2}. \end{align}$
Eliminating $h$ and solving for $x$ gives $x=1/2.$ Let $E$ be the symmetric image of $B$ in $D.$ Then, on one hand, $\angle CEB=\beta.$ On the other hand, $CE=CB=4,$ making $\Delta ACE$ isosceles such that $\angle ACE=\angle CAE=\alpha.$ It follows from the External Angle Theorem that
$\beta =\angle CEB =\angle ACE+\angle CAE = 2\alpha,$
as required.
Solution 2
Let's the bisector $BL$ of $\angle ABC.$
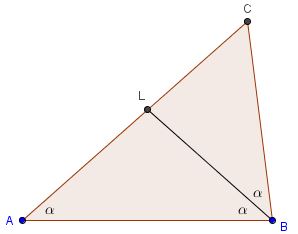
Let, as usual, $AB=c,$ $AC=b,$ and $BC=a,$ $p=(a+b+c)/2.$ Then by a known formula
$\displaystyle BL=\frac{4p(p-b)ac}{(a+c)^2}.$
For the given side lengths ($a=4,$ $c=5,$ $b=6),$ $\displaystyle BL=\frac{10}{3}.$
Now, apply a property of angle bisectors
$\displaystyle \frac{CL}{AL}=\frac{BC}{AB}=\frac{4}{5}.$
It follows that
$\displaystyle \frac{AC}{AL}=\frac{CL}{AL}+1=\frac{9}{5},$
i.e., $\displaystyle AL=\frac{6\times 5}{9}=\frac{10}{3}.$ In other words, $AL=BL,$ implying
$\alpha=\angle BAL=\angle LBA = \frac{1}{2}\angle ABC=\frac{1}{2}\beta.$
Solution 3
By the Law of Cosines, $\cos\alpha=3/4$ and $\cos\beta=1/8$: $\beta=2\alpha$ follows then from $\cos\beta=2\cos^2\alpha-1$ and the double angle formula $\cos 2\alpha=2\cos^2\alpha-1.$
Remark
It appears that other formulas from triangle geometry may help solve that problem. For example, from Heron's formula one can find the area $S$ of the triangle and then the altitude from $C$ which offers a different starting point for Proof #1.
Knowing the area, we may also find the circumradius: $abc=4RS$, and then apply the Law of Sines to obtain $\displaystyle\sin\alpha=\frac{\sqrt{7}}{4}$ and $\displaystyle\sin\beta=\frac{3\sqrt{7}}{8}.$ With these we may then continue as in Proof #3.
Acknowledgment
The problem and the first solution are from Jim Totten's Problems of the Week. Solution #3 is by Grégoire Nicollier.
References
- J. G. McLoughlin et al, Jim Totten's Problems of the Week, World Scientific, 2013, #329
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73571667
