|
|

|
|Store|
|

|

|

|
|

|

|

|

CTK Exchange
alexb
Charter Member
1040 posts |
Jul-18-03, 06:36 PM (EST) |
    |
1. "RE: Drop a normal"
In response to message #0
| |
>To drop a normal from a point to a line, the well known
>construction requires using the compass 3 times. Is it
>possible to drop a normal using the compass less than 3
>times? It's J. Steiner's theorem that in the presence of a circle and its center any construction is possible with a straightedge alone. So you need to use compass only once. Note that if there is a square present in the plane a circle is not needed. So, in principle, your problem may be solved with 0 or 1 compass applications. The construction is particularly simple with 2 compass applications. >If yes, how is it done? One needs to use the compass twice to draw a random line perpendicular to the given one and not passing through the given point. Nothing is need but a straightedge to draw a line through a point parallel to the given line not passing through the point. |
|
|
|
Printer-friendly page | Top |
|
|
 |
Vladimir
Member since Jun-22-03
|
Jul-18-03, 11:47 PM (EST) |
    |
2. "RE: Drop a normal"
In response to message #1
| |
Oho, I did not have a clue that I was theoretically covered. It is not possible to drop a normal to a line without the use of the compass. Proof: Suppose such construction is possible and let's call it the construction Q. Let's have a circle without the center. Draw a chord at random (we are getting close to the Bertrand's paradox!!!!). The chord intersects the circle at points A and B. Use the construction Q to drop a normal to the chord from any point. Using the straight edge alone, draw a parallel of this line through the point A (or B). The parallel is normal to the chord and intersects the circle at another point C. This gives us a right angle triangle ABC. Its hypotenuse is the circle diameter. Repeat the whole process with another chord selected at random (here I go again!!!) This gives us another diameter of the circle. The 2 diameters intersect in the center of the circle. We found the center of the circle using the straight edge alone. However, according to Jacob Steiner's theorem, this is impossible. A contradiction. The construction Q is impossible. Using the compass 2 times was too easy. How is it done using the compass only once? (I have probably given up too much). |
|
|
|
Printer-friendly page | Top |
|
|
|
 |
alexb
Charter Member
1040 posts |
Jul-18-03, 11:58 PM (EST) |
    |
3. "RE: Drop a normal"
In response to message #2
| |
>It is not possible to drop a normal to a line without the
>use of the compass. Well, if there's a square in the plane, you do not need a compass at all. >Using the compass 2 times was too easy. How is it done using
>the compass only once? (I have probably given up too much). The most fundamental construction is drawing a line through a point parallel to a line. Call it (*). Now, pick a point and draw a circle with that point as a center. Next choose a point on the circle and use (*) for that point. This gives you a chord, with the endpoints, say, A and B, parallel to the given line. Connect A to the center and extend that line to past the center to the intersection with the circle at, say, D. BD is then perpendicular to the given line. Apply (*) to the given point and BD.
|
|
|
|
Printer-friendly page | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Jul-19-03, 07:51 AM (EST) |
    |
4. "RE: Drop a normal"
In response to message #3
| |
I cannot figure out the supposed construction of drawing a line through a point parallel to a given line using the straight edge only (I hope it is not shifting triangle shaped rulers against each other). Do you know how to do it or just that it exists? This is the construction for dropping a normal using the compass once: Suppose the point P is not on the line. Select an arbitrary point on the line, say Q. Draw a circle with center at the point Q and with an arbitrary radius greater than QP (i.e., the given point P is inside the circle). The circle intersects the line at points A and B. Connect points A and B with the point P and extend these lines to intersect the circle at points A' and B', respectively. Connect points A with B' and B with A'. This gives us two right angle triangles DABB' and DABA'. Extend the lines AB' and BA' beyond the points B' and A', respectively. They intersect at the point C. Now we have DABC and its 2 altitudes AA' and BB' intersecting at the given point P, the orthocenter of this triangle. Connect point C with P and extend to the given line. CP is the 3rd altitude. 
Unfortunately, the construction fails if the point P is on the given line - I cannot erect a normal.
|
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f19175b2364e715.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f19175b2364e715.gif
|
|
|
Printer-friendly page | Top |
|
|
|
 |
alexb
Charter Member
1040 posts |
Jul-19-03, 08:33 AM (EST) |
    |
5. "RE: Drop a normal"
In response to message #4
| |
LAST EDITED ON Jul-19-03 AT 08:41 AM (EST)
>I cannot figure out the supposed construction of drawing a
>line through a point parallel to a given line using the
>straight edge only (I hope it is not shifting triangle
>shaped rulers against each other). Do you know how to do it
>or just that it exists? It goes in 3 steps.
- Draw a line parallel to a given line. (See https://www.cut-the-knot.org/Curriculum/Geometry/ParallelLinesAndSimilarTriangles.shtml) - Later note: Oops, sorry about that. While the construction is possible, the particular example is only midly relevant. I am thinking of that.
- Given two parallel lines and a segment on one of them, divide the segment in two. (Think of a trapezoid and the line through the midpoints of its bases.)
- Given a segment and its midpoint, and a point away from the line of the segment, draw a line through the point parallel to the segment. (Reverse #2.)
|
|
|
|
Printer-friendly page | Top |
|
|
|
 |
alexb
Charter Member
1040 posts |
Jul-19-03, 09:35 AM (EST) |
    |
6. "RE: Drop a normal"
In response to message #5
| |
LAST EDITED ON Jul-19-03 AT 09:38 AM (EST)
1. Draw a line parallel to a given line. (See
https://www.cut-the-knot.org/Curriculum/Geometry/ParallelLinesAndSimilarTriangles.shtml)
- Later note: Oops, sorry about that. While the
construction is possible, the particular example is only
midly relevant. I am thinking of that.
Now that I think of it, the construction of a line parallel to another line with a ruler is in fact impossible, unless there's some shape to depend on. I must begin to think of retirement - such a blooper!
But the fact is you do not need that. The question was to drop a perpendicular with a single compass usage. I reduced the problem to drawing a parallel line instead of a normal. You can draw a parallel line in the presence of a circle and its center. See Dorrie's book for the construction. My apologies.
|
|
|
|
Printer-friendly page | Top |
|
|
|
 |
|
 |
|
 |
Vladimir
Member since Jun-22-03
|
Jul-23-03, 05:21 PM (EST) |
    |
10. "RE: Draw a parallel"
In response to message #9
| |
I figured out the construction to draw a parallel to a given line through a given point P using the compass once, but I cannot come up with anything using the square. 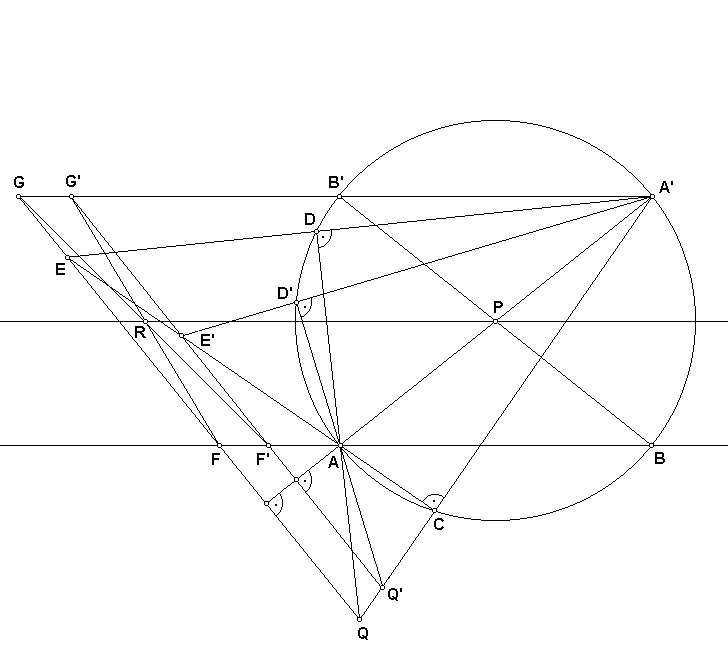
1. Draw a circle with the center at the point P and an arbitrary radius greater than the distance of the point P from the given line. The circle intersects the line at points A and B. Draw lines AA' and BB' through the circle center P. Line B'A' is parallel to the given line AB. 2. Select an arbitrary point Q not on the circle and not on line AA'. Construct a normal to the line AA': Draw a line from Q to A' intersecting the circle at point C draw another line from Q through A intersectng the circle at point D. Connect C with A and A' with D, extending the lines until they intersect at point E. We have DQA'E with all 3 altitudes and orthocenter A. Therefore QE is perpendicular to AA'. Select another point Q' at random, for example on the line QA' (to simplify the construction) and similarly drop a normal from Q' to the line AA'. 3. Lines QE and Q'E', being both normal to the same line AA', are parallel. They intersect the parallel lines AB and B'A', forming a parallelogram FF'GG'. Construct diagonals FG' and F'G of this parallelogram. The diagonals intersect at point R. Connect points P and R by a line. PR is parallel to the given line AB through the given point P. P.S. I was anxiously waiting for your comments on the proof that a triangle construction from angle bisectors is impossible. Actually, I was trying to construct the damn triangle for about a week before the impossibility proof dawned on me. |
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f1ef7cf3db30669.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f1ef7cf3db30669.gif
|
|
|
Printer-friendly page | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Jul-31-03, 08:38 AM (EST) |
    |
11. "RE: Drop a normal"
In response to message #9
| |
I am not 100% sure how the square drawing tool should work. I assume that the square center and its half-diagonal may be selected (just like the circle center and its radius with a compass). Selecting the half-diagonal implies that one vertex may be placed on a given line or into a given point. If this is the case, then the idea behind dropping a normal from a given point P to a given line using the square drawing tool once is quite simple (even though I had a hard time to find it): Using the symetry of the square, reflect 2 different lines passing through the point P in the given line. The mirror images of the 2 lines intersect at the mirror image of the point P and the line connecting the point P with its mirror image is perpendicular to the given line. 
1. Select an arbitrary point Q on the given line. Draw a square with the center at the point Q and with an arbitrary half-diagonal QA, placing the vertex A on the given line. Label it ¨ABCD. 2. Connect the point P with the opposite square vertex D (opposite with respect to the given line). Line PD intersects the square diagonal AC (coincident with the given line) at the point E. Draw a line from the opposite square vertex B through the point E and extend it beyond the point E. Line BE is a mirror image of the line PD (blue lines). 3. Connect the point P with the more distant square vertex C placed on the given line. Line PC intersects the square diagonal BD (perpendicular to the given line) at the point F. Draw a line from the opposite square vertex A through the point F and extend it beyond the point F. Line AF intersects the square side BC at the point G. Draw a line from the point G through the square center Q and extend it beyond the point Q. Line GQ intersects the square side DA at the point H. Draw a line from the square vertex C through the point H and extend it beyond the point H. Line CH is a mirror image of the line PC (red lines). 4. Lines BE and CH intersect at the point R, a mirror image of the point P with respect to the given line. Connect the points P and R. Line PR is the desired normal (green line).
|
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f28c3ab621d5a7c.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f28c3ab621d5a7c.gif
|
|
|
Printer-friendly page | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Jul-31-03, 08:38 AM (EST) |
    |
12. "RE: Drop a normal"
In response to message #9
| |
LAST EDITED ON Jul-31-03 AT 11:17 AM (EST)
Once a normal is dropped using the square drawing tool once, the parallel to a given line through a given point P can be constructed using the same idea as in constructing a parallel using the compass once: Using the symetry of the square, construct some parallel to the given line. Drop 2 normals from 2 different arbitrary points to the square diagonal. The 2 pairs of parallel lines form a parallelogram. Line connecting its center (the diagonal intersection) with the given point P is the desired parallel.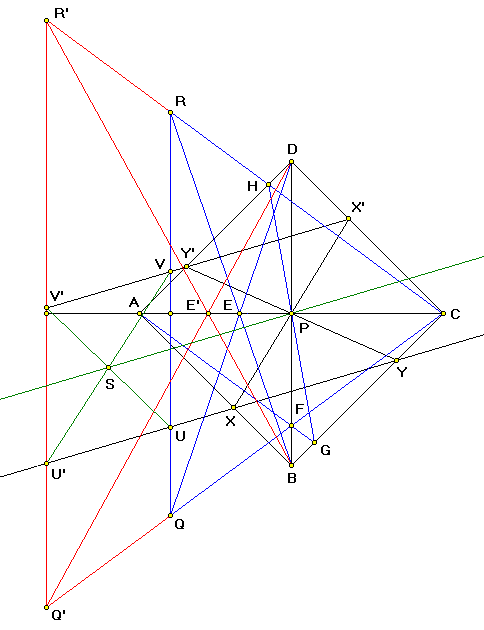
1. Draw a square ¨ABCD with center at the given point P and with an arbitrary half-diagonal PA longer than the distance of the point P from the given line. 2. The square sides AB and BC intersect the given line at the points X and Y, respectively. Connect the point X with the square center P and extend beyond until the line XP intersects the square side CD at the point X'. Connect the point Y with the square center P and extend beyond until the line YP intersects the square side DA at the point Y'. Line Y'X' is parallel to the given line XY. 3. Drop a normal from an arbitrary point Q to the square diagonal AC: Connect the point Q with the opposite square vertex D. Line QD intersects the square diagonal AC at the point E. Draw a line from the square vertex B opposite to D through the point E and extend beyond. Connect the point Q with the distant square vertex C. Line QC intersects the square diagonal BD at the point F. Draw a line from the square vertex A opposite to C through the point F and extend beyond until it intersects the square side BC at the point G. Draw a line from the point G through the square center P and extend beyond until it intersects the square side DA at the point H. Draw a line from the distant square vertex C through the point H and extend beyond until it intersects the line BE at the point R. Point R is a mirror image of the point P with respect to the square diagonal AC and the line PR is perpendicular to this diagonal. Select another arbitrary point Q', for example on the line QC (to simplify the construction), and similarly drop a normal from this point to the square diagonal AC. 4. Lines QR and Q'R', being perpendicular to the same line AC, are parallel. If they do not intersect the parallel lines XY and Y'X', the square diagonal BD is the desired parallel to the given line XY through the point P. Otherwise, the parallel lines QR and Q'R' intersect the parallel lines XY and Y'X', forming the parallelogram UVV'U'. Construct the diagonals UV' and VU' of this parallelogram. They intersect at the parallelogram center S. Connect the point S with the given point P. Line PS is the desired parallel to the given line XY through the point P.
|
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f28e1013f1a71c6.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f28e1013f1a71c6.gif
|
|
|
Printer-friendly page | Top |
|
|
|
 |
|
 |
Vladimir
Member since Jun-22-03
|
Jul-31-03, 12:02 PM (EST) |
    |
14. "RE: Drop a normal"
In response to message #13
| |
I am aware that none of the above construction, with a circle or with a square, is exactly what the Steiner theorem states. In the compass constructions I chose the circle center to be on a given line (drop a normal), the circle radius with respect to an arbitrary center (erect a normal), or the circle center at a given point (draw a parallel). Similarly, in the square constructions, I chose the square center and one square vertex to be on a given line (drop a normal) or the square center in a given point (draw a parallel). A normal has not been erected yet with the square. These constructions are a good step. The next step should be to perform these constructions with either one arbitrary circle with the known center or one arbitrary square, more complicated constructions and a greater challenge. But in ordinary geometrical constructions it is up to me to place the circle center in a selected point and/or select its radius (one choice is sometimes given up, being arbitrary, but never both). Similarly, I started with the square constructions and tried to imagine how such a square drawing tool (an analogy to the compass) might work. Well, how do you think it might work? |
|
|
|
Printer-friendly page | Top |
|
|
|
 |
alexb
Charter Member
1040 posts |
Jul-31-03, 12:25 PM (EST) |
    |
15. "RE: Drop a normal"
In response to message #14
| |
>challenge. But in ordinary geometrical constructions it is
>up to me to place the circle center in a selected point
>and/or select its radius (one choice is sometimes given up,
>being arbitrary, but never both). Right, because a compass is available. >Similarly, Not at all. >I started with
>the square constructions and tried to imagine how such a
>square drawing tool (an analogy to the compass) might work.
>Well, how do you think it might work? You do not know how to draw a square with a straightedge. >Well, how do you think it might work? Do not know. Here are the basic constructions with a straightedge:
- Given a line L and three points on that line: A, B, C, such that C is the midpoint of AB. Given a point P away from the line. Draw a line through P parallel L.
- Given two parallel lines L and M and a point P not on either L or M. Draw a line through P parallel to L and M.
- Given a parallelogram, a line L and a point P not on L. Draw a line through P parallel to L.
- Given a square. Construct its center.
- Given a square and a line through its center. Errect a perpendicular to the line through the center of the square.
- Given a square, a line L and a point P. Drop a perpendicular from P to L.
Answer to #6.
- Through the center of square draw a line parallel to the given one (use #3). Call the line S.
- Errect a perpendicular to S through the center of the square (use #5). Call it T.
- Through P draw a line parallel to T (use #3).
Answer to #5. Given a square ABCD with center O and a line FOG, where, say, F lies on AB and G lies on CD. Through F draw a line parallel to BC and AD (#2). Let H be the intersection of that line with CD. Through H draw a line parallel to AC (#3). Let K be its intersection with AD. KO is perpendicular to FG. |
|
|
|
Printer-friendly page | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Jul-31-03, 04:16 PM (EST) |
    |
16. "RE: Drop a normal"
In response to message #15
| |
LAST EDITED ON Jul-31-03 AT 05:17 PM (EST)
#4 is trivial and #5, #6 are solved using #2, #3. Here is solution of #2 using #1:
Draw 2 arbitrary lines from the point P, both intersecting the given parallels L and K. Denote the intersections on the parallel K as A, B and the intersections on the parallel L as C, D. Construct the diagonals of the trapezoid ABDC. They intersect at the point O. Draw a line from the point P through the point O, intersecting the parallels K and L at points Q and R, respectively. Claim: AQ = BQ
CR = DR reducing the #2 basic straightedge construction to the #1 basic straightedge construction. Proof: 1. DAQO is similar to DDRO and consequently AQ/QO = DR/RO
DR = RO·AQ/QO 2. DBQO is similar to DCRO and consequently BQ/QO = CR/RO
CR = RO·BQ/QO 3. DAQP is similar to DCRP and consequently AQ/PQ = CR/PR 4. DBQP is similar to DDRP and consequently BQ/PQ = DR/PR Combining 2. with 3. and 1. with 4.: AQ = PQ·CR/PR = PQ·BQ·RO/{QO·PR}
BQ = PQ·DR/PR = PQ·AQ·RO/{QO·PR} Dividing the two equations: AQ/BQ = BQ/AQ
AQ2 = BQ2
AQ = BQ and similarly for CR = DR. Q.E.D. Working on the #1 and #3 basic straightedge constructions.
|
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f2979ec13afc5d1.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f2979ec13afc5d1.gif
|
|
|
Printer-friendly page | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Jul-31-03, 08:52 PM (EST) |
    |
17. "RE: Drop a normal"
In response to message #15
| |
LAST EDITED ON Aug-01-03 AT 01:41 AM (EST)
#1 basic straight edge construction looks like an inverted #2 basic straightedge construction, but the proof is different:
Points A, B, and the midpointt C of AB on the line L (AC = BC). Draw a line from point P through the point A and another line through point B. Draw an arbitrary line through the midpoint C such that it intersects the line PA below (point E) and the line PB above (point F)the line L. Connect points A and F and extend beyond F. Connect points E and B and extend beyond B. Lines AF and EB intersect at the point R. Line K = PR is parallel to the line L = AB. Proof: Suppose we have a parellel K' to the line L, possibly different fron the constructed line K, and that this parallel K' intersects the lines AF and EB at 2 different points: RA º K' ´ AF and RB º K' ´ EB, which are of course different from the constructed intersection R º AF ´ EB. 1. DEPRB is similar to DEAB. Therefore: EP/EA = ERB/EB
EP/EA - 1 = ERB/EB - 1
(EP - EA)/EA = (ERB - EB)/EB
PA/EA = BR/EB PA/EA·EB/BR = 1 2. Point G is the intersection of the lines K' and CF (G º K' ´ CF). DECA is similar to DEGP and DECB is similar to DEGRB. Therefore: AC/PG = EC/EG = BC/RBG.
Since AC = BC, PG = RBG and RBG/GP = 1 3. Combining 1. and 2: PA/EA·EB/BR·RBG/GP = 1 By Ceva's theorem for DEPRB, lines PB, EG, and RBA are concurrent, the point of concurrence being the intersection of the lines EC (same as EG) and PB. Consequently, lines AR and ARB are identical, points R, RB, and RA are identical, and the constructed line K is identical with the parallel K'. Q.E.D. Working on #3 basic straightedge construction. P.S.
"You do not know how to draw a square with a straightedge."
I never said that I can. Since the square appears to be as good as the circle for all geometrical constructions (and I mean constructions where we use the compass liberaly or where we limit ourselves to one use of the compass but still choose the center, the radius, or both), what would be acceptable and what would not for constructions using the square instead. With the straightedge, we cannot measure. With the compass, we cannot touch a line - the point of touch has to be constructed. The question was whether choosing the square center, half-diagonal, and direction of one vertex would be the proper limitation.
|
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f29b5c92791312d.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f29b5c92791312d.gif
|
|
|
Printer-friendly page | Top |
|
|
|
 |
alexb
Charter Member
1040 posts |
Jul-31-03, 09:07 PM (EST) |
    |
18. "RE: Drop a normal"
In response to message #17
| |
>P.S.
>"You do not know how to draw a square with a straightedge."
>I never said that I can. No, not in so many words. You just wanted to place the square where you found it convenient. I am telling you that a square is given, period. It's not up to you to draw it or shift it. >Since the square appears to be as
>good as the circle for all geometrical constructions (and I
>mean constructions where we use the compass liberaly or
>where limit ourselves to one use of the compass but still
>choose the center, the radius, or both), what would be
>acceptable and what would not for constructions using the
>square instead. These are two different problems:
- Construct such-and-such with a single application of compass.
- Construct such-and-such, given a circle and its center.
Constructions with a given square are like #2, not #1. (However, everything that can be done with #1 can also be done with #2.) >With the straightedge, we cannot measure.
>With the compass, we cannot touch a line - the point of
>touch has to be constructed. The question was whether
>choosing the square center, half-diagonal, and direction of
>one vertex would be the preoper limitation. No, it's not what I meant. From Littlewood's Miscellany: Teacher: Assume X is the number of sheep in a flock.
Student: But assume X is not the number of sheep in the flock. Post factum it's all the same. It does not matter where the center of the square is located, what is its orientation or side length. Still, unless those facts have been previously established, which takes ##1-6, you can't place a square at your convenience while proving those basic constructions.
|
|
|
|
Printer-friendly page | Top |
|
|
|
 |
Vladimir
Member since Jun-22-03
|
Aug-01-03, 03:41 AM (EST) |
    |
19. "RE: Drop a normal"
In response to message #15
| |
#3 basic straightedge construction: Given a parallelogram ABCD, a line L, and a point P, draw a parallel to the line L through the point P. 
1. Construct diagonals AC and BD of the parallelogram ABCD. They intersect at the parallelogram center O, dividing each other in half: AO = CO
BO = DO 2. Select 2 parallel (opposite) sides of the parallelogram (does not matter which pair), say AD and BC. Line L intersects AD at the point E and line BC at the point F. The lines AD and BC can be extended if necessary. 3. Select one parallelogram diagonal (does not matter which one), say BD. Using #1 basic construction, construct a line parallel to this diagonal through the point E and intersecting the opposite parallelogram side BC at the point G. Using #1 basic construction again, construct a line parallel to the same diagonal through the point F and intersecting the opposite parallelogram side AD at the point H. Parallel lines BC = FG, AD = HE and parallel lines EG, HF bound a new parallelogram EHFG. 4. The given line L is coincident with the diagonal EF of the new parallelogram. Contruct the other diagonal GH. The diagonals EF and GH intersect at the parellogram center S, dividing each other in half: ES = FS
GS = HS 5. Using #1 basic construction, construct the line K parallel to the diagonal EF (coincident with the given line L) through the given point P. Proof is not necessary. Lines L and K are parallel by construction. #5 and #6 basic straightedge constructions: 
In the #5 basic straightedge construction at the left, line EG parallel to the square side AD is constructed using #2 basic straightedge construction. The rest is trivial. In the #6 basic straightedge construction at the right, line K through the square center O parallel to the given line L is constructed using #2 basic straightedge construction. Normal N to the line K at the circle center O is erected using #5 basic straightedge construction. Parallel to the normal N through the given point P is constructed using #3 basic straightedge construction (just as you said). |
Attachments
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f2a0c331251a4d4.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f2a0c331251a4d4.gif
 https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f2a0c5e127d23d6.gif
https://www.cut-the-knot.org/htdocs/dcforum/User_files/3f2a0c5e127d23d6.gif
|
|
|
Printer-friendly page | Top |
|
|
|

You may be curious to have a look at the old CTK Exchange archive.
Please do not post there.

|Front page|
|Contents|
Copyright © 1996-2018 Alexander Bogomolny
73582207
|
|
|