Parallel Lines and Similar Triangles:
What is it about?
A Mathematical Droodle

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Explanation

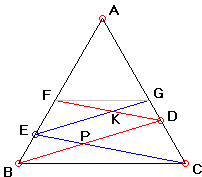
The problem is: in ΔABC draw lines BD and CE with D on AC and E on AB. Let F on AB and G on AC be such that DF||CE and EG||BD. Then FG||BC.

Let K be the intersection of DF and EG.

We may detect several pairs of similar triangles and derive several proportions. We need just two. Since triangles ABD and AEG,

AE/AB = AG/AD.

Since triangles ACE and ADF are similar, we have also

AF/AE = AD/AC.

The product of two proportions is

AF/AB = AG/AC,

which proves the claim.

Here's a more difficult problem related to the above. We shall consider lines parallel to concurrent Cevians.

Pick a point in the plane and the Cevians through that point. Draw a line parallel to the base to the intersections with the sides. From those two points draw parallels to the Cevian through the apex till they intersect the base. From the two points on the base draw lines parallel to the other two Cevians and then procede as in the first problem. The top line is always parallel to the base.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72083906