Problem 5 from the third round
of the 17th USAMTS 2005-2006
(USAMTS stands for the USA Mathematical Talent Search, a math competition in its 17th year. Problem 5/3/17.)
Lisa and Bart are playing a game. A round table has n lights evenly spaced around its circumference. Some of the lights are on and some of them off; the initial configuration is random. Lisa wins if she can get all of the lights turned on; Bart wins if he can prevent this from happening.
On each turn, Lisa chooses the positions at which to flip the lights, but before the lights are flipped, Bart, knowing Lisa’s choices, can rotate the table to any position that he chooses (or he can leave the table as is). Then the lights in the positions that Lisa chose are flipped: those that are off are turned on and those that are on are turned off. Here is an example turn for n = 5 (a white circle indicates a light that is on, and a black circle indicates a light that is off):
| Initial Position. | 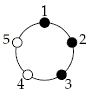 |
| Lisa says "1, 3, 4." Bart rotates the table one position counterclockwise. | 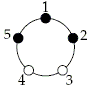 |
| Lights in positions 1, 3, 4 are flipped. | 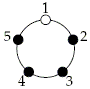 |
Lisa can take as many turns as she needs to win, or she can give up if it becomes clear to her that Bart can prevent her from winning.
Credit: This problem was based on a problem from the Puzzle TOAD page at https://www.cs.cmu.edu/puzzle. They credit the problem to Ron Holzman of the Technion-Israel Institute of Technology.
Comments: The case n = 7 can be solved by considering what moves must make Bart lose to Lisa. The case n = 8 can be solved by an induction argument. Solutions edited by Naoki Sato.
Solution 1 by: Hannah Alpert (11/CO)
For part (a), Lisa sees at least one light on and at least one light off, and she wants to turn all the lights the same color (we will say that two lights are the "same color if they are both on or both off). For Lisa to win, the game must end with Bart being stuck: He must either turn all the off lights on or all the on lights off. Then as a last move, if all the lights are off, Lisa will turn all of them on.
However, since 7 is odd, the number of off lights cannot be the same as the number of on lights. Therefore, Bart cannot end up with such a decision; for example, if there are 3 lights on and 4 lights off, and Lisa picks three positions, Bart cannot possibly be forced to turn all the lights the same color, because it is not even possible to turn all the off lights on! Thus, for any odd n and not all lights the same color, Bart can prevent Lisa from winning.
For part (b), we will prove by induction on k that if there are n = 2k lights, Lisa can always win in at most 2k turns. Then obviously, we can apply this fact to the case where
In the base case, k = 0, there is one light. If it is on, Lisa wins; if it is off, Lisa requests to turn it on. That takes only one turn.
Now assume that if there are 2k lights, then Lisa can win in at most 2k turns. We want to show that if there are 2×2k lights, then Lisa can win in at most 2×2k turns. Observe that since the number of lights,
Lisa's aim will be first to get each light the same color as its partner and then to turn all the pairs on. To get each light the same color as its partner, she restricts her choices such that she never chooses both a light and its partner. Since there are 2×2k lights, there are 2k sets of partners. Lisa imagines an equivalent table with 2k lights, where each light corresponds to one set of partners on the big table. For each pair on the big table that has two different colors, their light is off on the small table; for each pair on the big table with the same color, their light is on at the small table. Then she makes each light the same color as its partner in 2k moves, just as she would solve the small table in 2k moves.
[Ed: To clarify, here is an example. Suppose the big table has 8 lights, and positions 1, 2, and 6 are on. Then the small table has 4 lights, and positions 2, 3, and 4 are on. Looking at the small table, Lisa chooses position 1. That means on the big table, she can choose position 1 or 5. After she does so and Bart rotates the table, exactly one light (among two partners) is flipped, which means that one light gets flipped on the small table. Choosing exactly one light among partners ensures that this will always be the case. Lisa continues making moves towards getting all the lights on the small table, and when that happens, for any pair of partner lights on the big table, both are on, or both are off.]
Once every light is the same color as its partner, Lisa restricts her choices such that for every light she chooses, she also chooses its partner. This time she imagines another table with 2k lights. On this small table, each light still corresponds to one set of partners on the big table, but this time the light at the small table is the same color as the pair (since the partners now match). She finishes solving the big table in 2k moves, just as she would solve the small table in 2k moves. Lisa has then solved the big table with 2×2k lights in 2×2k moves. Our induction is complete.
Solution 2 by: Kristin Cordwell (9/NM)
(b) We identify the lights and the switching patterns with polynomials by calling the first of the consecutive eight lights (points) 1, the second x, the third x2, and so on, all the way up to x7. A light will be "on if the coefficient of its respective power of x is 1; otherwise, the light will be "off. We will also think of the switching pattern being rotated, rather than the lights. Similarly, a coefficient of 1 in a switching pattern polynomial will indicate
that that position is to be switched. To rotate a switching pattern n positions, we multiply the corresponding polynomial by xn, and we take this new polynomial
[Ed: For example, suppose the table has 8 lights, and positions 1, 2, and 6 are on. Then the polynomial corresponding to this set of lights is
x1 - 1 + x2 - 1 + x6 - 1 = 1 + x + x5.
Lisa chooses positions 1, 2, and 6. Suppose Bart rotates the table by five positions. Then the lights in positions 6, 7, and 3 get flipped, so the lights in positions 1, 2, 3, and 7 are on. In terms of the polynomials, we multiply 1 + x + x5 by
(1 + x + x5)(1 + x5) = 1 + x + 2x5 + x6 + x10.
We reduce all coefficients mod 2, because flipping a light twice does nothing. Also, going around the circle, position 10 is the same as position 2, which is the same as reducing the polynomial
| 1 + x + 2x5 + x6 + x10 | ≡ 1 + x + x2 + x6 |
| = x1 - 1 + x2 - 1 + x3 - 1 + x7 - 1, |
which confirms that the lights at positions 1, 2, 3, and 7 are on.]
An(x) the polynomial for the lights at the end of the nth round. We claim that if Lisa gives Bart a switching pattern equal to the "on lights at the beginning of that round, then Lisa will win in eight or fewer rounds.
When Lisa gives Bart A0(x) for the switching pattern, we end up with
A1(x) = An(x) + xa1An(x) = (1 + xa1)An(x)
as the new light pattern, where Bart has rotated the switching pattern by a1 positions. Similarly,
A2(x) = (1 + xa2)A1(x),
where Bart rotates the second switching pattern by a2 positions. Continuing, we get
A3(x) = (1 + xa3)A2(x),
A4(x) = (1 + xa4)A3(x),
. . . ,
A8(x) = (1 + xa8)A7(x).
Note that if x = 1, then for any i,
1 + xai = 1 + 1ai = 2 ≡ 0,
so
|
| |
| = 1 + 2x + 2x2 + ... + 2xai - 1 + xai | |
| ≡ 1 + xai |
Thus, setting Pi(x) = 1 + x + x2 + ... + xai - 1, we can write
1 + xai ≡ (1 + x)Pi(x).
So,
| A8(x) | = (1 + xa8)A7(x) |
| = (1 + xa8)(1 + xa7)A6(x) | |
| = ... | |
| = (1 + xa8)(1 + xa7) ... (1 + xa1)A0(x) | |
| ≡ (1 + x)P8(x)(1 + x)P7(x) ... (1 + x)P1(x)A0(x) | |
| = (1 + x)8P8(x)P7(x) ... P1(x)A0(x). |
Now,
| (1 + x)8 | = 1 + 8x + 28x2 + 56x3 + 70x4 + 56x5 + 28x6 + 8x7 + x8 |
| ≡ 1 + x8 (reducing the coefficients mod 2) | |
| ≡ 0, (reducing the polynomial mod 1 + x8) |
so A8(x) = 0. Therefore, all lights will always be off after eight rounds. Looking back at the equation
A8(x) = (1 + xa8)A7(x),
we see that the polynomial A7(x) must then have the property that for any a8, multiplying
A7(x) by
A7(x) = 1 + x + x2 + ... + x7.
Thus, after seven turns, the lights are either all on or all off. If the lights are all on, Lisa has won at the end of the seventh round (or sooner, if they were all on sooner). If they are all off, Lisa gives Bart the switching pattern of change everything, and Lisa wins at the end of the eighth round (or sooner, if they were all off sooner). This generalizes to all n that are powers of two, so that Lisa can always win in at most n rounds.
Generating Functions
- Generating Functions
- A Property of the Powers of 2
- An USAMTS problem with light switches
- Examples with series of figurate numbers
- Euler's derivation of the binary representation
- Examples with finite sums with binomial coefficients
- Fast Power Indices and Coin Change
- Number of elements of various dimensions in a tesseract
- Straight Tromino on a Chessboard
- Ways To Count
- Probability Generating Functions
- Finite Sums of Terms 2^(n-i) i^2
- Sylvester's Problem, a Second Look
- Generating Functions from Recurrences
- Binet's Formula via Generating Functions
- Number of Trials to First Success
- Another Binomial Identity with Proofs
- Matching Socks in Dark Room
|Contact| |Front page| |Contents| |Games|
Copyright © 1996-2018 Alexander Bogomolny73564709
