The Squeeze Theorem

The Squeeze (or Squeezing) Theorem is an extremely useful and conceptually transparent tool of calculus.

Theorem

Proof of the Squeeze Theorem

Given $\epsilon\gt 0,$ choose $\delta_{g}\gt 0$ and $\delta_{h}\gt 0$ such that for all $x\ne a$ that satisfy $|x-a|\lt\delta_{g},$ $|g(x)-L|\lt\epsilon,$ and, respectively, all $x\ne a$ that satisfy $|x-a|\lt\delta_{h},$ $|h(x)-L|\lt\epsilon.$ With $\delta=\min\{\delta_{g},\delta_{h}\},$ we have that, for all $x\ne a$ that satisfy $|x-a|\lt\delta,$ we have both inequalities $|g(x)-L|\lt\epsilon$ and $|h(x)-L|\lt\epsilon,$ which informs us that

$-\epsilon\lt g(x)-L\lt f(x)-L\lt h(x)-L\lt \epsilon,$

i.e., $|f(x)-L|\lt\epsilon,$ which exactly means that $\displaystyle\lim_{x\rightarrow a}f(x)=L.$

As an example of application, I'll use the Squeeze theorem to prove the continuity of functions $\sin\theta$ and $\cos\theta.$

$\sin\theta$ is continuous at $\theta =0.$

Consider a unit circle (the circle of radius $1$) and small angle (arc) $\theta\gt 0.$

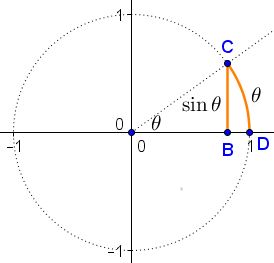
The area of $OBC$ equals $\frac{1}{2}BO\cdot BC=\frac{1}{2}\sin\theta.$ The area of sector $ODC$ equals $\frac{1}{2}\theta.$ Since the triangle is contained in the sector, its area is smaller: $\sin\theta\lt\theta.$

So far $\theta$ was thought of as positive. If we allow for negative angles, then, since sine is an odd function $(\sin(-\theta)=-\sin\theta),$ $|\sin\theta |\lt |\theta |,$ at least for $\theta$ close to $0.$ We may rewrite this as

$|\sin\theta - 0|\lt |\theta - 0|.$

This actually shows that $\displaystyle\lim_{\theta\rightarrow 0}\sin\theta =0.$ Indeed, to use the definition, pick small $\epsilon\gt 0$ and set $\delta =\epsilon.$ The above inequality makes it obvious that $|\theta - 0|\lt\delta$ implies $|\sin\theta - 0|\lt\epsilon,$ exactly as required for the continuity of $\sin\theta$ at $\theta =0,$ because, by definition, $\sin 0=0.$

The Squeeze Theorem, offers a detour, if not a shortcut: the quantities in the diagram are positive so that $0\lt\sin\theta\lt\theta.$ Obviously, $\displaystyle\lim_{\theta\rightarrow 0}\theta =0.$ In particular, $\displaystyle\lim_{\theta\rightarrow 0^{+}}\theta =0,$ i.e., if $\theta$ is positive. Thus, it follows from the Squeeze Theorem that $\displaystyle\lim_{\theta\rightarrow 0^{+}}\sin\theta =0.$ But, since $\sin\theta$ is odd, we also have $\displaystyle\lim_{\theta\rightarrow 0^{-}}\sin\theta =0,$ the two combine in the required $\displaystyle\lim_{\theta\rightarrow 0}\sin\theta =0.$

$\cos\theta$ is continuous at $\theta =0.$

Augment our diagram with $DE\perp OC$ and $EG\perp OD.$

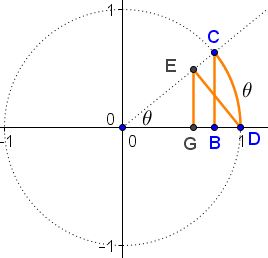
By symmetry, $OE=OB=\cos\theta$ and, so $OG=\cos^{2}\theta =1-\sin^{2}\theta.$ The diagram sets up for the application of the Squeeze Theorem:

$1-\sin^{2}\theta\lt\cos\theta\lt 1$

Note that from the properties of the limit,

$\displaystyle\lim_{\theta\rightarrow 0^{+}}(1-\sin^{2}\theta ) = 1-(\lim_{\theta\rightarrow 0^{+}}\sin\theta)^{2}=1-0=1,$

implying $\displaystyle\lim_{\theta\rightarrow 0^{+}}\cos\theta =1.$ Since $\cos\theta$ is an even function, we at once obtain the required $\displaystyle\lim_{\theta\rightarrow 0}\cos\theta =1$ which, together with $\cos 0=1$ proves the continuity of $\cos\theta$ at $x=0.$

$\sin\theta$ is continuous for any (real) $\theta.$

The proof of continuity of $\sin\theta$ and also of $\cos\theta$ (which I omit) is done by pure algebra. Recollect the addition formulas:

$\sin(\alpha \pm\beta )=\sin\alpha\cos\beta\pm\sin\beta\cos\alpha.$

The assertion that for some $\theta_{0},$ $\displaystyle\lim_{\theta\rightarrow\theta_{0}}\sin\theta =\sin\theta_{0}$ is equivalent to saying that $\displaystyle\lim_{\tau\rightarrow 0}\sin(\theta_{0}+\tau) =\sin\theta_{0}.$ So, try

$\begin{align} \displaystyle \lim_{\tau\rightarrow 0}\sin(\theta_{0}+\tau) &=\lim_{\tau\rightarrow 0}(\sin\theta_{0}\cos\tau+\sin\tau\cos\theta_{0})\\ &=\sin\theta_{0}\lim_{\tau\rightarrow 0}\cos\tau+\cos\theta_{0}\lim_{\tau\rightarrow 0}\sin\tau\\ &=\sin\theta_{0}\cdot 1+\cos\theta_{0}\cdot 0\\ &=\sin\theta_{0}, \end{align}$

as required.

$\cos\theta$ is continuous for any (real) $\theta.$

The continuity is proved similarly based on addition formulas for cosine:

$\cos(\alpha \pm\beta )=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta.$

Note 1: there is another, a more exciting application of the Squeeze Theorem.

Note 2: the above implicitly assumes that the notion of the area of a sector or the length of an arc are well defined. As the matter of fact they are, and the Squeeze Theorem plays an important role in their definitions.

|Contact| |Front page| |Contents| |Algebra|

Copyright © 1996-2018 Alexander Bogomolny