An Equation Involving Four Collinear Points

Here's a problem by Leo Giugiuc that was offered at the 2015 Romanian Regional Olympiad for grade 10 (Problem 3.)

Leo supplied the first three solutions. I have added one more, and Grégoire Nicollier added the fifth, one line, solution. Later Leo sent a solution by Seclaman Dan Radu.

Solution 1

Note that

(1)

$|z-2i|=|\frac{2}{5}(z-5i)+\frac{3}{5}z|\le \frac{2}{5}|z-5i|+\frac{3}{5}|z|.$

Similarly,

(2)

$\displaystyle |z-3i|\le \frac{3}{5}|z-5i|+\frac{2}{5}|z|.$

The combination of (1) and (2) tells us that

(3)

$|z|+|z-5i|\le |z-2i|+|z-3i|.$

Now, we have an equality in (3) only if both (1) and (2) are equalities which requires

(4)

$\overline{z}(z-5i)\ge 0.$

Let $z=a+bi,$ $a,b\in\mathbb{R}.$ Then (4) becomes $(a-bi)(a+bi-5i)\ge 0,$ i.e., $a^{2}+b(b-5)-5ai\ge 0.$ This is only possible when $a=0,$ implying $b(b-5)\ge 0.$ This is equivalent to $b\lt 0$ or $b\gt 5.$

Thus the solution is the set $\{bi:\; b\lt 0\;\mbox{or}\;b\gt 5\}.$

Solution 2

This solution makes use of the well-known Hlawka's inequaility:

(5)

$|x+y|+|y+z|+|z+x|\le |x|+|y|+|z|+|x+y+z|$

which holds for any there complex numbers $x,y,z$ (and has an analog in vector spaces with scalar product.) To use the inequality rewrite (*) as

$|z|+|-2i|+|-3i|+|z-5i|=|z-2i|+|-2i-3i|+|z-3i|.$

By Hlawka's inequaility,

$|z|+|-2i|+|-3i|+|z-5i|\ge |z-2i|+|-2i-3i|+|z-3i|$

which is (3).

For there to be equality, it is necessary that $\overline{(ab)}c(a + b + c)\ge 0.$ So, setting $a = -2i,$ $b = -3i$ and $c = z$ we have to require $\overline{(2i\cdot 3i)}z(z - 5i)\ge 0,$ or $z(z - 5i)\ge 0.$ Let $z = a + bi,$ where $a,b\in\mathbb{R}.$ Then $(a + bi)[a + (b - 5)i]\ge 0,$ or equivalently, $a=0$ and $b(b - 5)\ge 0$ which gives $b\in (-\infty , 0] \cup [5, \infty).$

Solution 3

Here's a more general formulation:

Using vectors, we have $\overrightarrow{MB} = k\overrightarrow{MA} + (1 - k)\overrightarrow{MD},$ where $k \in (0 , 1).$ $\overrightarrow{MC} = k\overrightarrow{MD} + (1 - k)\overrightarrow{MA}.$ It follows that

(6)

$MB = |\overrightarrow{MB}| = |k\overrightarrow{MA} + (1 - k)\overrightarrow{MD}| = kMA + (1 - k)MD$

and, similarly

(7)

$MC = kMD + (1 - k)MA.$

Combining (6) and (7) gives

(8)

$MB + MC \le MA + MD.$

(8) becomes an equality only if (6) and (7) are equalities, i.e., when vectors $\overrightarrow{MA}$ and $\overrightarrow{MD}$ are collinear and have the same orientation. This is exactly equivalent to $M\in d\setminus \{AD\}.$

Solution 4

As in the Solution #3, the four points $A,B,C,D$ need not lie on the $y$-axis, but may be collinear on any lie. For convenience I choose the $x$-axis, with points $A,B,C,D$ having coordinates $a,b,c,d,$ respectfully (so that $a\lt b\lt c\lt d).$ The situation is reminiscent of an optimization problem of building a house on a straight road. I start with giving a general formulation:

Let point $M$ in the plane have coordinates $(x,y).$ Assume $AB=CD.$ Then (**) holds if and only if $y=0$ and $x\in (-\infty, a]\cup [d,\infty).$

First we establish that for points outside the $x$-axis the equality in (**) cannot hold. Let $M'$ be the reflection of $M$ in the midpoint of $AD,$ or $BC,$ which is the same because $AB=CD:$

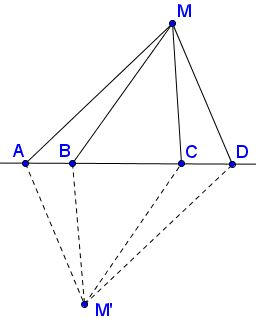
By the construction, the parallelogram $MBCM'$ is located entirely within the parallelogram $MADM'$ such that its perimeter is less than that of the latter:

$2(BM+CM)\lt 2(AM+DM).$

Thus, we have only inspect points $M$ on the $x$-axis. For $b\le x\le c,$ $BM+CM=c-b$ while $AM+DM=d-a.$ The latter still holds for, say $a\lt x\lt b.$ However,

$\begin{align} MB+MC &= (b-x)+(c-x)\\ &\lt (b-a)+[(c-b)+(b-x)]\\ &\lt [(b-a)+(c-b)]+(b-a)\\ &\lt (c-a)+(d-c)\\ &=d-a\\ &=AM+DM. \end{align}$

By analogy, the equality in (**) can't hold for $c\lt x\lt d$ either. Let now $x\le a.$ In this case,

$\begin{align} MB+MC &= (b-x)+(c-x)\\ &= (b-a)+ (c-a)+2(a-x)\\ &= (d-c)+ (c-a)+2(a-x)\\ &= (d-a)+2(a-x)\\ &= (d-x)+(a-x)\\ &=AM+DM, \end{align}$

and, similarly, for $x\ge d.$

Solution 5

The solutions are the points common to two ellipses with the same major axis and are thus the possible end points of the major axis.

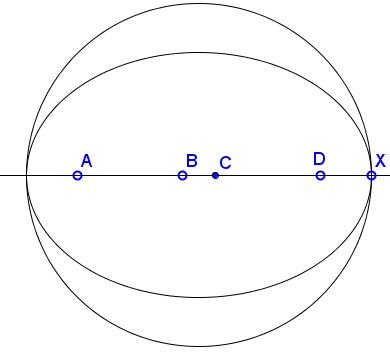
Solution 6

Square the two sides of (*) to obtain first

$z\cdot\overline{z} + (z - 5i)(z + 5i) + 2|z^{2}-5iz| = (z - 2i)(z + 2i) + (z - 3i)(z + 3i) + 2|z^{2} - 5iz - 6|.$

which is then simplified to

$|z^{2}-5iz| + 6 = |z^{2} - 5iz - 6|.$

Denoting $Z=z^{2}-5iz$ we obtain $|Z|+6=|Z-6|.$ Due to the triangle inequality, this implies that $Z$ is real and not positive: $Z\in\mathbb{R}$ and $Z\le 0.$ Thus, for $z$ we have a quadratic equation $z^{2} - 5iz=a\le 0,$ with a real $a.$ Solving this equation we obtain

$\displaystyle z=\frac{5i\pm\sqrt{-25+4a}}{2}=\frac{i}{2}(5\pm\sqrt{25-4a})=Ai,$

where $A=\displaystyle\frac{1}{2}(5\pm\sqrt{25-4a}),$ $a\le 0.$ Choosing sign "+" gives $A=\displaystyle\frac{1}{2}(5+\sqrt{25-4a})\ge 5.$ Choosing sign "-" gives $A=\displaystyle\frac{1}{2}(5-\sqrt{25-4a})\le 0.$

|Contact| |Front page| |Contents| |Algebra|

 

Copyright © 1996-2018 Alexander Bogomolny