Perimeters of Convex Polygons, One within the Other

Let P(X) denote the perimeter of polygon X.

At first site the statement seems obvious, although in general it touches on fundamental and deep properties of geometric shapes. But the problem is not about arbitrary plane regions - it's about convex polygons, and this could be utilized to our advantage. More specifically, the statement yields to an elegant proof by induction. What you want to do is find a discrete parameter that would make the inductive step all but obvious.

We are given that S ⊂ T, but it does not mean that the two polygons may not share a side line. For example, in the diagram below side A'B' of S lies on side AB of T (and, therefore, A'B' is not longer than AB.) The same is true concerning sides C'D' and CD of S and T respectively.

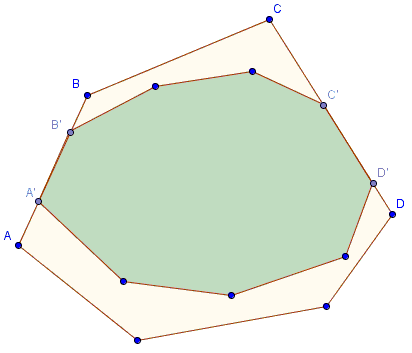
So S may or may not have some sides on the boundary of T. Let's agree to call sides of S that do not lie on any side of T free. The induction will be on the number of free sides of S.

If S has no free sides then each of its sides lies on a side of T and is, therefore, not longer than the latter. It follows that in this case P(S) ≤ P(T), and the equality is only possible when the two polygons coincide.

Now, for an inductive step, introduce statement X(k): "For two polygons S ⊂ T, with exactly k sides of S being free, P(S) < P(T)" and assume that X(k) is true for some k ≥ 0. We wish to prove that then X(k+1) is also true.

So let this be the case that S has k+1 free sides. Since k+1 > 0, S has at least one free side. Extend this side until the line meets the boundary of T:

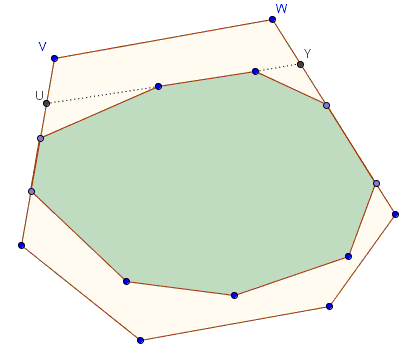
That line will split T into two, say, T' and T''. As we know, convex polygon are the intersections of half planes and so always lie on one side from their side lines, implying that S may belong to only one of T' or T''. Let it be T': S ⊂ T'. Importantly, P(T') < P(T) due (with a reference to the above diagram and the triangle inequality) to the fact that the straight line segment UY is shorter than the broken line UVWY. The second important observation is that, relative to T', S has one less (i.e., k) free sides than relative to T. By the inductive assumption P(S) < P(T') so that, to, P(S) < P(T), as promised.

This is an example from a Russian book Simplest Examples of Mathematical Proofs by V. A. Uspensky (MCCME, 2009.)