Candido's Identity

Giacomo Candido (1871-1941) has invented a formula that seems to have been published posthumously ten years after his death:

\((x^{2}+y^{2}+(x+y)^{2})^{2}=2(x^{4}+y^{4}+(x+y)^{4})\).

The formula can be easily verified by carrying through the operations involved. There is also a proof without words by Alsina and Nelsen:

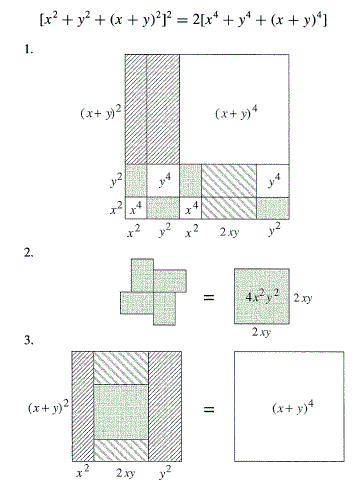
Candido's formula - a proof without words

Candido applied the formula to establishing a property of the Fibonacci numbers:

\((F_{n-1}^{2}+F_{n}^{2}+F_{n+1}^{2})^{2}=2(F_{n-1}^{4}+F_{n}^{4}+F_{n+1}^{4})\).

The formula is little known - I found it mentioned only in a recent book by R. Grimaldi.

Alsina and Nelsen generalized the question by asking for solutions \(f\) of the functional equation

\(f(f(x) + f(y) + f(x + y)) = 2 [f(f(x)) + f(f(y)) + f(f(x + y))].\)

They proved that, assuming \(f\) is continuous function from \([0,\infty)\) onto \([0,\infty)\) such that \(f(0) = 0\), the solution is unique (up to a constant factor), \(f(x)=x^2\). There are really great many discontinuous solutions. Any \(f\) with the property that \(f(x) =0\) for rational \(x\) and \(f(x)\) rational (but arbitrary!), otherwise, satisfies the generalized equation!

R. S. Melham extended the property of the Fibonacci numbers by showing (among others) that

\(2(F_{n}^{2}+F_{n+1}^{2}+F_{n+2}^{2}+F_{n+3}^{2})^{2}=3(F_{n}^{4}+F_{n+1}^{4}+F_{n+2}^{4}+F_{n+3}^{4})^{4}\).

References

C. Alsina, R. B. Nelsen, Candido's Identity, Mathematics Magazine, Vol. 78, No. 2 (Apr., 2005), p. 131
C. Alsina, R. B. Nelsen, On Candido's Identity, Mathematics Magazine, Vol. 80, No. 3 (Jun., 2007), pp. 226-228
G. Candido, A Relationship Between the Fourth Powers of the Terms of the Fibonacci Series, Scripta Mathematica, 17:3-4 (1951) 230
R. Grimaldi, Fibonacci and Catalan Numbers: an Introduction, Wiley, 2012
R. S. Melham, YE OLDE FIBONACCI CURIOSITY SHOPPE REVISITED, Fibonacci Quarterly, 2004, 2, 155-160

Fibonacci Numbers

Golden Ratio in Geometry

72199708