Outline Mathematics
Geometry

Two Altitudes, One Midpoint:
What Is This About?

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Discussion

|Up| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet attempts to suggest the following problem:

In triangle ABC, AE and BD are the altitudes to sides BC and AC, respectively. M is the midpoint of AB. Prove that MD = ME .

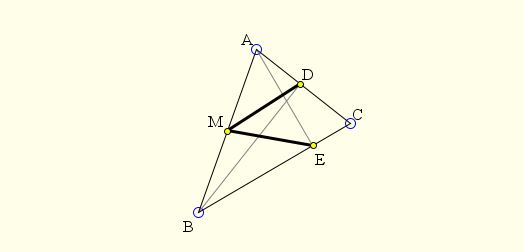
Two Altitudes One Midpoint

This is a frequently employed argument: since triangle ABD is right,equilateral,scalene,isosceles,right,equilateral, its circumcircle has AB as the diameter,radius,diameter,segment,chord,sector. The same is true of triangle ABE, meaning that the four points A, B, D, E are concyclic,concyclic,collinear,coalesced,harmonic. Moreover, the circumcircle of the four points has AB as the diameter and M as the center.

In other words, D and E both lie on circle C(M, AB/2) with center M and radius AM = BM = AB/2. This exactly means that MD = AB/2 = ME.

Related material
Read more...

  • Orthogonality in Isosceles Triangles
  • Midpoints and Orthogonality in Isosceles Triangles
  • A Median in Touching Circles
  • Square, Similarity and Slopes

    • |Up| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71226052