Square, Similarity and Slopes
The following problem was twitted around by David Radcliffe:
\(ABCD\) is a square. Point \(E\) is on side \(AB\) or its extension. \(F\) is the intersection of \(DE\) and \(BC\). \(G\) is the intersection of \(AF\) and \(CE\). Prove that \(BG\) is perpendicular to \(DE\).
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny\(ABCD\) is a square. Point \(E\) is on side \(AB\) or its extension. \(F\) is the intersection of \(DE\) and \(BC\). \(G\) is the intersection of \(AF\) and \(CE\). Prove that \(BG\) is perpendicular to \(DE\).
| What if applet does not run? |
Solution
Depending of where point \(E\) is relative to \(AB\) there are three possible configurations. The same idea applies in all three cases. I shall consider only one where point \(E\) is to the right from \(B\).
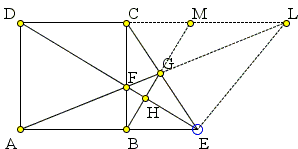
Extend \(AG\) and \(BG\) to their intersection with \(CD\) at \(L\) and \(M\), respectively. This generates several pairs of similar triangles. I'll use the similarities to determine the slopes of \(BG\) and \(DE\). To start with,
\begin{align} slope(DE) & = -AD/AE, \\ slope(BG) & = BC/CM. \end{align}
Triangles \(CGM\) and \(EGB\) are similar and so are triangles \(LGM\) and \(AGB\). From here,
\[ \frac{CM}{BE} = \frac{GM}{BG} = \frac{LM}{AB}. \]
Triangles \(DCF\) and \(EBF\) are also similar and so are triangles \(CLF\) and \(BAF\), so that
\[ \frac{CL}{AB} = \frac{CF}{BF} = \frac{CD}{BE} = \frac{AB}{BE}. \]
Or,
\[ \frac{AB}{BE} = \frac{CM + LM}{AB} = \frac{CM}{AB} + \frac{CM}{BE}. \]
This can be rewritten as
\[ AB^2 = CM(AB + BE) = CM\cdot AE. \]
And, finally,
\[ 1 = \frac{AB}{CM} \cdot \frac{AB}{AE} = \frac{BC}{CM} \cdot \frac{AD}{AE}, \]
which is the same as
\[ slope(DE)\cdot slope(BG) = -1, \]
implying that the two lines are orthogonal.
Related material
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73573714
