Outline Mathematics
Geometry

Triangle Areas in a Parallelogram II

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

This is a generalization of a one hundred years old problem.

If from any point in a diagonal of a parallelogram lines are be drawn to the opposite angles the parallelogram will be divided into two pairs of equivalent triangles.

The problem appeared in a periodical publication Mathematical Visitor and then included into a recent collection under the same name. It took the broadcast power of internet for the problem to reach overseas and a generalization emerge. Floor van Lamoen, The Netherlands, has noticed that point M does not have to lie on a diagonal of the parallelogram for there to be two pairs of triangles with equal sum of areas.

So let M be any point inside parallelogram ABCD. Triangles AMB and CMD have equal bases: AB = . The sum of their altitudes ME + MF = is fixed and does not depend on point M. We have

Area(AMB) + Area(CMD)	= AB·ME/2 + CD·MF/2
	= AB·ME/2 + AB·MF/2
	= AB·(ME + MF)/2
	= AB·EF/2
	= .

It follows that the remaining area, Area(BMC) + Area(AMD) is also Area(ABCD)/2. So that the two are equal.

Matt Henderson came up with an even simpler solution:

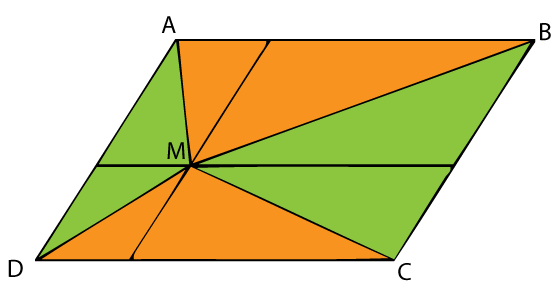
The two lines through point M parallel to the sides of the parallelogram cut the latter into four smaller parallelograms. Each of these is divided by the diagonal from M into two (green and orange) equal areas.

References

1. S. Rabinowitz (ed), Problems and Solutions from the Mathematical Visitor (1877-1896), MathPro Press, 1996

|Up| |Contact| |Front page| |Contents| |Geometry| |Store|