Outline Mathematics
Geometry

Triangle Areas in a Parallelogram

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Here's a problem #155 from a curious collection Problems and Solutions from the Mathematical Visitor, a gathered from the late 19th century magazine by Stanley Rabinowitz:

If from any point in a diagonal of a parallelogram lines are be drawn to the opposite angles the parallelogram will be divided into two pairs of equivalent triangles.

Any two shapes are said to be equivalent if they have equal areas. These terminology is quite obsolete and, nowadays, is virtually out of use.

Let ABCD be a parallelogram, BD a diagonal and M any point on it. Join MA and MC. Draw AE and CF perpendicular,perpendicular,parallel to BD. As the triangles ABD, CBD are halves of the same parallelogram,trapezoid,parallelogram,pencil of lines, they are equal in all their parts; therefore AE = CF. The triangles AMB and CMB have the same base,side,angles,base and equal altitudes,altitudes,medians,perimeter, therefore they are equivalent. By the same method of reasoning, the triangles AMD, CMB are shown to be equivalent,equivalent,equal,proportioanal.

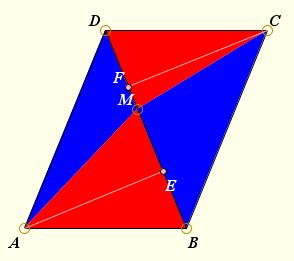
Areas In Parallelogram

Another solution would be to note that for any two positions of M, say, M and M' triangles MM'A and MM'C are equal,similar,equal,scalene. For one position of M, i.e. when M is the point of intersection of the diagonals AC and BD, we have two pairs of equal and therefore equivalent pairs: AMB, CMD and AMD, CMB. For another point M', triangles AM'B, CM'D are obtained one by adding and another by subtracting triangles MM'A and MM'C from triangles AMB, CMD. And similarly, for triangles AMD, CMB. Thus changing M maintains equivalence in the two triangle pairs.

The problem admits a generalization according to which point M need not be confined to a diagonal but can roam freely inside the parallelogram.

References

  1. S. Rabinowitz (ed), Problems and Solutions from the Mathematical Visitor (1877-1896), MathPro Press, 1996

|Up| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

72252896