Perimeters of Parallelogram And Rhombus
What Is This About?
6 May 2016, Created with GeoGebra
Problem
The parallelogram with maximum perimeter for given diagonals is a rhombus.
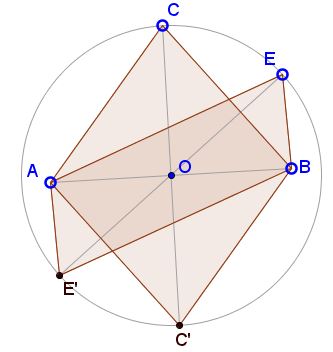
Proof 1
Assume one of the diameters (the vertical one in the diagram below) has length $2b,\;$ the other one $2a.\;$ Denote the angle between the two $\alpha.$
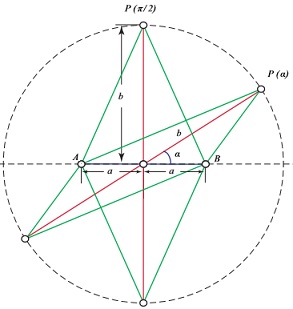
Using the Law of Cosines, we need to prove that
$\begin{align} |AP(\alpha )|+|BP(\alpha)| &= \sqrt{a^2+b^2+2ab\cos\alpha}+\sqrt{a^2+b^2-2ab\cos\alpha}\\ &\le 2\sqrt{a^2+b^2}. \end{align}$
But this follows from the AM-QM inequality.
Proof 2
Form an ellipse $\epsilon\;$ with foci $A\;$ and $B\;$ such that, for a generic point $E\;$ on the ellipse, $AE+BE=AC+BC,$ where $C\;$ is the apex of the isosceles triangle $ABC.$ Let $O\;$ be the midpoint of $AB\;$ and the center of both the circle $(O)=C(O,OC)\;$ and of the ellipse $\epsilon.$
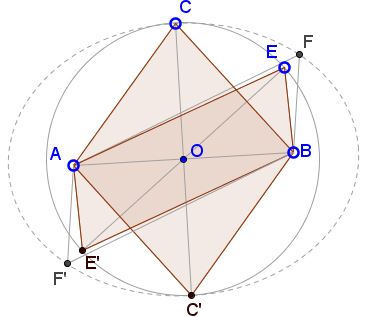
Since the foci of an ellipse lie on its major axis, the circle $(O)\;$ has as its diameter the minor axis of the ellipse and is therefore located within the ellipse. If $F\;$ and $F'\;$ are the points of intersection of the diagonal $EE'$ of the parallelogram $AE'BE\;$ with $\epsilon\;$ then $AC+BC=AF+BF\ge AE+BE.\;$ This is because the perimeter of a convex polygon lying within another polygon does not exceed the perimeter of the latter.
References
The statement and Proof 1 are by Angel Plaza, see The Parallelogram with Maximum Perimeter for Given Diagonals Is the Rhombus—A Proof Without Words and a Corollary, Math. Mag. 88 (2015) 360–361
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73574781
